A K. 297. feladat (2011. szeptember)

K. 297. Az ábrán látható módon egy téglalap jobb felső sarkából kivágtunk egy négyzetet. Az így kapott síkidom területe 2011 cm².

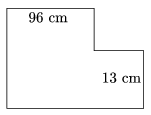
Mekkora az eredeti téglalap területe?

(6 pont)

A beküldési határidő 2011. október 10-én LEJÁRT.

Megoldás. A kivágott négyzet oldalának hosszát jelöljük \(\displaystyle x\)-szel. Ekkor a síkidom területére fennáll, hogy \(\displaystyle (96+x)(13+x)-x^2=2011\). Rendezés után \(\displaystyle 109x=763\), ahonnan \(\displaystyle x=7\). Ennek segítségével az eredeti téglalap területe \(\displaystyle (96+7)(13+7)=2060\) \(\displaystyle cm^2\).

Statisztika:

340 dolgozat érkezett.
6 pontot kapott:	302 versenyző.
5 pontot kapott:	4 versenyző.
4 pontot kapott:	1 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	7 versenyző.
0 pontot kapott:	22 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2011. szeptemberi matematika feladatai