A K. 305. feladat (2011. október)

K. 305. Amerika csapadékban szegény részeinek műholdas felvételét nézegetve érdekes köröket láthatunk (pl. Texasban, a 79068 ZIP-kódú területen, a Google Earth programban a kereséshez TX 79068-at írva.) A körök abból a sajátos öntözési technológiából származnak, melyben egy rúd alakú öntözőberendezés forog körben a középpontja vagy az egyik vége körül. Természetesen így a földterület egy része termelésre nem használható, mert a víz nem mindenütt éri el, csak a körökön belül.

Joe, Jim és Jack három testvér, mindhármójuknak 1 km oldalhosszúságú, négyzet alakú földjük van. Az öntözött területet az ábrán látható módon alakították ki:

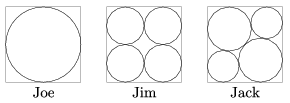
Jack elrendezésében a kisebbik körök sugara 210,5 m. Melyikük elrendezése a leghatékonyabb, azaz melyikük tudja földjének legnagyobb részét növénytermesztésre használni?

(6 pont)

A beküldési határidő 2011. november 10-én LEJÁRT.

Megoldás. Joe öntözőkörének sugara \(\displaystyle 500\ m\), így ő \(\displaystyle 500^2\cdot \pi \approx 785398\ m^2\) nagyságú területet tud öntözni és termelni rajta. Jim egy öntözőkörének sugara \(\displaystyle 250\ m\), de négy van belőle, ezért az által öntözött terület nagysága \(\displaystyle 4 \cdot 250^2\cdot \pi \approx 785398\ m^2\), megegyezik Joe-éval. Jack nagyobbik körének sugarát az alábbi ábra alapján számíthatjuk ki, felhasználva, hogy a négyzet átlójának hossza \(\displaystyle \sqrt 2\)-ször annyi, mint az oldalának hossza:

Jelölje \(\displaystyle x\) a nagyobbik kör sugarát. A nagy négyzet átlója \(\displaystyle 2x+2y\), ahol \(\displaystyle y=\sqrt 2 x\) (mert \(\displaystyle y\) az \(\displaystyle x\) oldalú négyzet átlója), azaz \(\displaystyle x = \frac{1000\sqrt 2}{2\sqrt 2 +2}\approx 292,9\ m\). A négy kör együttes területe: \(\displaystyle 2\cdot 292,9^2\cdot \pi+2\cdot 210,5^2\cdot \pi \approx 817 032\ m^2\). Tehát Jack elrendezése a leggazdaságosabb hármójuké közül.

Megjegyzés: A műholdas képeken nem látunk olyan elrendezést, mint Jacké, és a körök is nagyjából egyformának tűnnek. Lehet, hogy a gyártók csak egységes méretben gyártják az öntöző berendezéseket, de az is lehet, hogy még senkinek nem jutott eszébe változatni.

(A kisebbik kör sugarához az ábrán középen látható derékszögű háromszöget használhatjuk fel. Ha a kis kör sugarát \(\displaystyle r\) jelöli, akkor az átfogó \(\displaystyle x+r\), a befogók \(\displaystyle x\) és \(\displaystyle \frac{1000\sqrt 2}{2}-z\), ahol \(\displaystyle z=\sqrt 2 r\). Felírva a Pitagorasz-tételt \(\displaystyle x^2 + (500\sqrt 2 -r\sqrt 2)^2 = (x+r)^2\), behelyettesítve és a kapott másodfokú egyenletet megoldva \(\displaystyle r \approx 210,5\ m\).)

Statisztika:

284 dolgozat érkezett.
6 pontot kapott:	90 versenyző.
5 pontot kapott:	20 versenyző.
4 pontot kapott:	7 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	132 versenyző.
1 pontot kapott:	17 versenyző.
0 pontot kapott:	9 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2011. októberi matematika feladatai