A K. 336. feladat (2012. március)

K. 336. Az ábrán látható konkáv 16-szöget négy egybevágó négyzetre és nyolc egybevágó rombuszra vágtuk, a rombuszok kisebbik szöge 45 fokos. Mekkora a 16-szög területe, ha a rombuszok hosszabb átlója 10,7 cm-es?

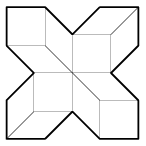
(6 pont)

A beküldési határidő 2012. április 10-én LEJÁRT.

Megoldás. A négyzetek és rombuszok oldalhossza legyen \(\displaystyle x\), akkor az ábrán jelölt szakasz hossza \(\displaystyle y=\frac{\sqrt 2}{2}x\), a rombusz hosszabbik átlójának hosszát beírva az alkalmazott Pithagorasz-tételbe: \(\displaystyle \left( 1+ \frac{\sqrt 2}{2}\right)^2 x^2 + \left(\frac{\sqrt 2}{2} x\right)^2=10,7^2\), azaz \(\displaystyle \left(1+\sqrt 2 + \frac{1}{2} + \frac{1}{2} \right)x^2=(2+\sqrt 2)x^2=10,7^2\), ahonnan \(\displaystyle x=5,79cm\) és \(\displaystyle y=4,09cm\). A síkidom területét számoljuk ki, mint egy \(\displaystyle 2x+2y\) oldalú négyzet területének és két \(\displaystyle x\) oldalú négyzet területének különbségét: \(\displaystyle 323,4~cm^2\).

Statisztika:

104 dolgozat érkezett.
6 pontot kapott:	Andrási Alex Gyula, Asbolt Máté, Bajnok Anna, Belényesi Máté, Csilling Tamás, Dóka Csilla Anna, Fekete Panna, Fényes Balázs, Geiszl András, Gnandt Balázs, Hanyu Krisztina, Hauber Júlia, Hegyi Zoltán, Heszler András, Holczer András, Hollós Bálint, Horváth 501 Cintia, Iványi Blanka, Jákli Aida Karolina, Király 719 Ágnes, Kling Anna, Kovács 148 Dávid, Kovácshegyi Kinga , Körmendi Tamás, Lőrincz Ádám Sándor, Maizl Noémi, Mándoki Sára, Markó Gergely, Marosi Petra Rita, Máté Bálint, Meskó Csaba, Mészáros Gabriella, Molnár 286 Soma, Olexó Tünde, Qian Lívia, Rátky Márton, Ruzicska György, Szakács Béla Benedek, Sziegl Benedek, Tamás Ambrus, Tamás Csongor, Tatár Krisztina, Tóth Ádám Bars, Tóth Adrián, Varga Dániel Kristóf, Virágh Anna, Weisz Szilvia.
5 pontot kapott:	27 versenyző.
4 pontot kapott:	7 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	16 versenyző.

A KöMaL 2012. márciusi matematika feladatai