A K. 385. feladat (2013. október)

K. 385. Egy négyzet alakú papírlapot összehajtottunk, majd egy egyenes vágással levágtunk az összehajtott papírból egy darabot. Amikor kihajtottuk, láthattuk, hogy egy négyzet alakú lyuk keletkezett a közepén az ábrának megfelelően (a két négyzet középpontja egybeesik, és a kis négyzet megfelelő oldalai párhuzamosak a nagy négyzet átlóival).

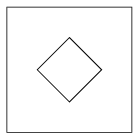
Adjunk meg egy megfelelő összehajtás és vágás kombinációt, amely a feladatban leírtakat eredményezi.

Adjunk meg egy olyan összehajtás-vágás kombinációt, amelyben a kivágott rész egy téglalap, de nem négyzet. (Az összehajtott papírlapból most is egy egyenes vágással vágunk le egy darabot, és a négyzet és a téglalap középpontja egybeesik, és a téglalap megfelelő oldalai párhuzamosak a négyzet átlóival.)

(6 pont)

A beküldési határidő 2013. november 11-én LEJÁRT.

Megoldás. Sok megoldás van. Érdemes visszafelé gondolkodni: kivágunk egy négyzetet (téglalapot), majd úgy hajtjuk össze a nagy négyzetet, hogy a kis négyzet (téglalap) oldalai egymásra kerüljenek.

Egy lehetséges megoldás Abonyi-Tóth Barbaráé (Budapest, ELTE Apáczai Csere János gyak. Gimn.):

Először az egyik átlója mentén félbehajtjuk:

és azt a két csúcsot, amelyeket ez az átló összeköt, az eredeti négyzet oldalára merőlegesen behajtjuk úgy, hogy mind a négy csúcs egy helyre kerüljön.

Ezután már csak a keletkezett négyzet felső sarkát (az eredeti négyzet közepét) az oldalakkal 45°-os szöget bezárva kell levágnunk.

Az előzőhez hasonlóan itt is először félbehajtjuk a lapot az átlója mentén, de mivel téglalapot akarunk belőle kivágni és nem négyzetet, ezért az egyik oldalát meg kell nyújtanunk az eredeti négyzet átlójával párhuzamosan,

ezért az átló által összekötött két csúcsot nem hajtjuk le egészen addig, hogy a négy csúcs összeérjen, hanem a hajtásvonal közelebb van az átló által összekötött csúcsokhoz, mint a másik kettőhöz.

Utolsó lépésként a keletkezett ötszög felső oldalát kell levágnunk a többi oldallal \(\displaystyle 45^{\circ}\)-os szöget bezárva.

Statisztika:

235 dolgozat érkezett.
6 pontot kapott:	111 versenyző.
5 pontot kapott:	29 versenyző.
4 pontot kapott:	38 versenyző.
3 pontot kapott:	33 versenyző.
2 pontot kapott:	18 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2013. októberi matematika feladatai