 |
A K. 39. feladat (2005. március) |
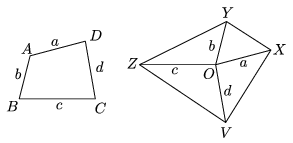
K. 39. Az ABCD konvex négyszög határoló vonalát csúcsainál szétvágjuk. A négy oldalszakaszt egy közös O pontba toljuk az ábrán látható módon, úgy, hogy párhuzamosak maradjanak eredeti helyzetükkel. Az oldalszakaszok O-tól különböző végpontjait összekötve egy XYZV négyszöget kapunk. Hányszorosa az XYZV négyszög területe az eredeti ABCD négyszögének?
(6 pont)
A beküldési határidő 2005. április 11-én LEJÁRT.
Megoldás. Nézzük azokat az oldalpárokat, amelyek mindkét elrendezésben rendelkeznek közös csúccsal, pl. a BC, CD és az YO, ZO párokat. Mivel ezek páronként párhuzamosak, a BCD és a ZYO háromszögek területe megegyezik, ugyanis pl. a c-vel jelölt oldalhoz tartozó magasság mindkettőben ugyanakkora. Ugyanígy az ADC és a VOZ háromszögek, a BAD és az XOV háromszögek, valamint az ABC és XOY háromszögek is azonos területűek. Az ABCD négyszög területét azonban az említett négy háromszög kétszer teszi ki, míg az XYZV négyszögét egyszer, ezért az utóbbi területe kétszerese az előbbiének.
Statisztika:
85 dolgozat érkezett. 6 pontot kapott: C. Szabó Bence, Gecse 666 Gergely, Győri Tamás Noé, Horváth Markó, Kapás Gábor, Károly Dóra, Kiss 103 Dániel , Marincsák Miklós, Matyuska Péter, Mihálykó Ágnes, Nagy 777 Mariann, Poócza Katalin, Szécsényi Ágnes, Szeles Annamária, Talabér Dóra, Tallián György, Tokai-Kiss Ákos, Tolner Ferenc. 5 pontot kapott: Balázs Attila, Gyurcsik Judit, Hoffmann Jenő, Kovács Blanka, Laki Balázs, Plesz Mónika, Sárvári Gábor. 4 pontot kapott: 11 versenyző. 3 pontot kapott: 21 versenyző. 2 pontot kapott: 10 versenyző. 0 pontot kapott: 18 versenyző.
A KöMaL 2005. márciusi matematika feladatai
