 |
A K. 424. feladat (2014. szeptember) |
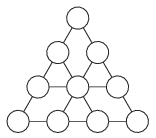
K. 424. Helyezzük el az alábbi ábrába az 1-10-ig terjedő egész számokat oly módon, hogy a pontosan négy számot tartalmazó szakaszokon levő számok összege 23 legyen (szakaszonként), a pontosan három számot tartalmazó szakaszokon levő számok összege pedig 16 (szakaszonként). Hány különböző elrendezés létezik? (A forgatásokkal és tükrözésekkel egymásba vihető elrendezéseket különbözőnek tekintjük.)
(6 pont)
A beküldési határidő 2014. október 10-én LEJÁRT.
Megoldás. Ha összeadjuk a három külső szakaszon álló 4-4 számot, továbbá a három belső szakaszon álló 3-3 számot, akkor minden számot pontosan kétszer, a középső számot viszont háromszor szerepeltettük az összegben, tehát ez az összeg az 1-től 10-ig terjedő számok összegének kétszeresénél a középen álló szám értékével lesz nagyobb. A megadott feltételeknek megfelelően ezen számok összege \(\displaystyle 3\cdot 23+3\cdot 16=117\), 1-10-ig a számok összege 55, tehát középen a 7 áll. Ahhoz, hogy a három számot tartalmazó szakaszokon 16 legyen az összeg, a 7-et kell kiegészítenünk két szám összegével 16-ra. azaz a két szám összegének 9-nek kell lennie. A fennmaradó számokból csak három olyan pár készíthető, melyek összege 9: 1+8, 3+6, 4+5, tehát a háromszög csúcsaiba a 2, 9, 10 számok kerülnek valamilyen sorrendben. A 9 és 10 közé kerülő két szám összege 4, ez csak az 1 és a 3 lehet. A 2 és a 9 közé eső két szám összege 12, ez csak a 8 és a 4 lehet, így a 2 és 10 közé marad az 5 és a 6. Mivel a három számot tartalmazó vonalakon levő párok is meg vannak határozva, ezért a 2, 9, 10 elhelyezése a fentiek szerint már meghatározza a többi szám helyzetét. Az összes lehetőségek számát tehát az határozza meg, hogy a háromszög csúcsaiban hányféleképpen helyezhető el a 2, a 9 és a 10. A felső csúcsba 3-féle, a jobb alsó csúcsba ezen belül kétféle szám kerülhet, tehát összesen hatféle különböző elrendezés létezik.
Statisztika:
103 dolgozat érkezett. 6 pontot kapott: Agócs Katinka, Korpás Isabel, Kós Anna, Kubovics Márton, Kulcsár Simon, Nagy Viktor, Németh Csilla Márta, Paulovics Péter, Sisák László Sándor, Slenker Balázs, Szarka Álmos, Tószegi Fanni, Valkó Bence, Wenczel Kata. 5 pontot kapott: Csuha Boglárka, Encz Koppány, Gyűrűs Boldizsár, Harsányi Benedek, János Zsuzsa Anna, Mihályházi Péter, Nagy Marcell, Páhoki Tamás. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 35 versenyző. 0 pontot kapott: 16 versenyző. Nem versenyszerű: 6 dolgozat.
A KöMaL 2014. szeptemberi matematika feladatai
