A K. 448. feladat (2015. január)

K. 448. Egy kör alakú tárcsán négy korong helyezkedik el az ábrának megfelelően. Hányféleképpen színezhetjük ki a korongokat négy szín segítségével, ha a tárcsa középpontja körüli, a tárcsa síkjában történő forgatással egymásba vihető színezéseket nem tekintjük különbözőnek? A színezéshez a négy színből tetszőlegesen választhatunk, egy korong egyszerre csak egy színnel színezhető.

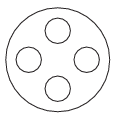
(6 pont)

A beküldési határidő 2015. február 10-én LEJÁRT.

Megoldás. Négy egyforma színnel nyilván 4 színezés létezik. Ha három egyforma szín van, az mindenképpen három szomszédos, azonos színű korongot és egy tőlük különböző színűt jelent. Az azonos színt 4-, a másikat 3-féleképpen választhatjuk ki, ami \(\displaystyle 4\cdot3=12\) lehetőség.

Ha két-két egyforma szín van, akkor az egyforma színek vagy szomszédosak, vagy szemköztiek, ez 2 lehetőség. A színeket mindkét esetben \(\displaystyle \binom42=6\)-féleképp választhatjuk ki. Ez \(\displaystyle 2\cdot6=12\) eset.

Ha két egyforma szín van, és összesen három szín, akkor az egyformák vagy szomszédosak, vagy szemköztiek. Ha szomszédosak, akkor \(\displaystyle 4\cdot3\cdot2=24\) színezés van, ha szemköztiek, akkor pedig \(\displaystyle 4\cdot\binom32=4\cdot3=12\).

Ha pedig négy különböző szín van, akkor az \(\displaystyle 4\cdot3\cdot2\cdot1\) lehetőség lenne, ám minden esetet 4-szer számolunk a forgatások miatt, vagyis ez igazából \(\displaystyle 3\cdot2=6\) lehetőség.

Mivel \(\displaystyle 4+12+12+24+12+6=70\), így 70-féleképpen színezhetjük ki a korongokat.

Statisztika:

79 dolgozat érkezett.
6 pontot kapott:	Agócs Katinka, Bärnkopf Teréz, Dévény Csaba, Dömötör Emőke, Farkas Lilla, Fazekas 15 Levente, Fekete Balázs Attila, Harsányi Benedek, Hegedűs 330 Marcell, Márton Anna, Nagy Marcell, Németh Csilla Márta, Oravecz Janka Éva, Páhoki Tamás, Papp 149 Emese, Sisák László Sándor, Szarka Álmos, Sziráki Boglárka Tünde, Tamási Kristóf Áron, Thuróczy Mylan, Tószegi Fanni, Wenczel Kata.
5 pontot kapott:	Braun Dániel, Cselovszki Tamás, János Zsuzsa Anna, Járomi Bence, Koronczi Fanni, Mészáros Melinda, Mihályházi Péter, Szakali Benedek, Walter Anna.
4 pontot kapott:	12 versenyző.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	17 versenyző.
0 pontot kapott:	10 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2015. januári matematika feladatai