A K. 507. feladat (2016. szeptember)

K. 507. Két ugyanakkora szabályos hatszögbe írtunk egy-egy hatágú csillagot, majd a csillagok belsejében keletkező kisebb szabályos hatszögbe ismét írtunk egy-egy hatágú csillagot. A csillagok csúcsai a megfelelő hatszög csúcsai, vagy oldalfelező pontjai voltak. Az elkészült rajzok az ábrán láthatók.

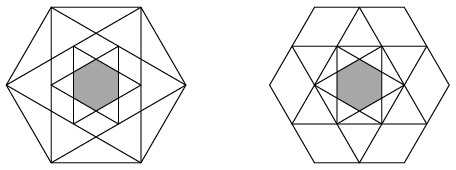
Hogy viszonyul egymáshoz a két kis besatírozott hatszög területe?

(6 pont)

A beküldési határidő 2016. október 10-én LEJÁRT.

Megoldás. Kétféleképpen írtunk szabályos hatszögbe csillagot. Mindkét csillag két szabályos háromszög ugyanolyan módon való egymásra helyezése, tehát hasonlóak. Az első módszerben a csillagot tartalmazó hatszög és a csillag csúcsai megegyeznek. Tekintsük a csillagba írt szabályos hatszöget. Legyen ekkor \(\displaystyle b\) a kisebb és a nagyobb hatszög területének aránya, vagyis \(\displaystyle t_{nagy~hatszög}\cdot b=t_{kis~hatszög}\). A második módszerben a csillag csúcsai a csillagot tartalmazó hatszög oldalfelező pontjai. Tekintsük ekkor is a csillagba írt szabályos hatszöget, jelölje ekkor \(\displaystyle c\) az előbbi arányt.

A bal oldali ábrán előbb az első módszert használjuk, majd a belső hatszögbe írunk egy kisebb csillagot a második módszer szerint, így a besatírozott hatszög területe \(\displaystyle t_{nagy~hatszög}\cdot b\cdot c\). A jobb oldali ábrán pedig először a második, majd a keletkező hatszögbe az első módszer szerint írtunk csillagot, ezért a satírozott hatszög területe \(\displaystyle t_{nagy~hatszög}\cdot c\cdot b\). Tehát a két hatszög területe egyenlő.

Statisztika:

100 dolgozat érkezett.
6 pontot kapott:	59 versenyző.
5 pontot kapott:	3 versenyző.
4 pontot kapott:	2 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	13 dolgozat.

A KöMaL 2016. szeptemberi matematika feladatai