A K. 599. feladat (2018. november)

K. 599. Helyezzük el a kis körökbe az 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 számokat úgy, hogy bármelyik négy, egy egyenesen fekvő körben lévő számok összege ugyanannyi legyen, sőt a csillag csúcsaiba írt számok összege is ezt a számot adja. Néhány számot előre beírtunk a körökbe. Adjuk meg az összes lehetséges kitöltést.

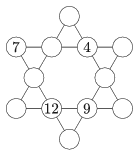
(6 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. Ha összeadjuk az összes vonalon lévő számokat, akkor a keresett összeg \(\displaystyle 6\)-szorosát kapjuk, és minden körben lévő számot kétszer számoltunk. Tehát az egy-egy vonalon álló négy szám összege \(\displaystyle \frac{1+2+3+... +12}{3}\). A \(\displaystyle 12\) és a \(\displaystyle 9\) mellé összesen \(\displaystyle 5\) kerül, ez csak \(\displaystyle 2+3\) formában tehető meg. A \(\displaystyle 7\) és \(\displaystyle 4\) mellé összesen \(\displaystyle 15\) kerül. A \(\displaystyle 3+12\), \(\displaystyle 4+11\), \(\displaystyle 6+9\), \(\displaystyle 7+8\) összegek egyik tagja már foglalt, így csak \(\displaystyle 5+10\) kerülhet a \(\displaystyle 7\) és \(\displaystyle 4\) mellé. Ha a \(\displaystyle 10\) a külső csúcsba kerülne, akkor a csúcsokba eddig biztosan bekerülő számok összege \(\displaystyle 7+10+3+2=22\) lenne, azonban ehhez már \(\displaystyle 4\)-et csak \(\displaystyle 1+3\) formában tudnánk adni, azonban a \(\displaystyle 3\) más foglalt. Tehát az \(\displaystyle 5\) kerül a hatszög külső csúcsába. Hasonlóan a \(\displaystyle 7+12\) mellé összesen \(\displaystyle 7\)-et kell írnunk, ez már csak \(\displaystyle 6+1\) formában lehetséges. Ha a \(\displaystyle 6\) kerülne a külső csúcsba, akkor a csúcsokban álló számok összege \(\displaystyle 7+6+2+3+5=23\) lenne, amihez \(\displaystyle 3\) kéne, de ez nem lehetséges. Így az \(\displaystyle 1\) kerül a külső körbe. Tehát most itt tartunk (a \(\displaystyle 2\) és a \(\displaystyle 3\) helyzete még nem dőlt el):

A külső csúcsokban az eddig szerepelő számok összege \(\displaystyle 7+2+1+3+5=18\), tehát a hiányzó szám a \(\displaystyle 8\). A \(\displaystyle 8+6+10=24\), tehát melléjük kerül a \(\displaystyle 2\), így a \(\displaystyle 3\) helyzete is megvan, az utolsó körbe pedig az eddig fel nem használt \(\displaystyle 11\) kerül.

Statisztika:

116 dolgozat érkezett.
6 pontot kapott:	Ágoston Schneider, Antal Botond, Bányai Kristóf, Barát Benedek, Cserkuti Sándor, Csoma Petra, Csuvár Ákos, Egyházi Hanna, Flódung Áron , Fonyódi Sára, Hamar János, Hamvas Johanna Kata, Hoffmann Szabolcs, Kalocsai Zoltán, Lajtos Enikő, Lévay Anna, Lukács Milán, Malatinszki Hanna, Márky Anna, Mátéfy Ádám , Metzger Ábris András, Miklóssy Katinka, Mócsy Mátyás, Mohay Lili Veronika, Németh László Csaba, Osváth Klára, Rács Zsóka, Riba Dániel, Ryan Voecks, Sámuel Laura , Sebestyén Pál Botond, Sipos Teodor, Solymosi Lili, Somogyi Dalma, Szabó 222 Benedek, Szatmáry Sára, Szépvölgyi Gergely, Szirmai Dénes, Tarján Teréz, Toronyi András, Varga 928 Péter, Xu Yiling.
5 pontot kapott:	16 versenyző.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	10 versenyző.
2 pontot kapott:	16 versenyző.
1 pontot kapott:	11 versenyző.
0 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	12 dolgozat.

A KöMaL 2018. novemberi matematika feladatai