A K. 651. feladat (2020. február)

K. 651. Az ábrán látható területekre teljesül, hogy \(\displaystyle T_1 : T_2 : T_3 = 2:7:3\). Mennyi az \(\displaystyle x\) és \(\displaystyle y\), illetve az \(\displaystyle u\) és \(\displaystyle v\) szakaszok aránya?

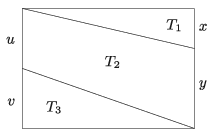
(6 pont)

A beküldési határidő 2020. március 10-én LEJÁRT.

Megoldás. Mivel \(\displaystyle T_1 : T_2 : T_3 = 2:7:3\), ezért legyen \(\displaystyle T_1 =2a\), \(\displaystyle T_2 =7a\), \(\displaystyle T_3 = 3a\). Rajzoljunk be két párhuzamos szakaszt az ábrán látható módon. A keletkező háromszögek területe megegyezik \(\displaystyle T_1\)-gyel, illetve \(\displaystyle T_3\)-mal, tehát \(\displaystyle 2a\)-val és \(\displaystyle 3a\)-val. A fennmaradó téglalap területe így \(\displaystyle (2a+7a+3a)-(2(2a+3a)=12a-10a=2a\).

A szaggatott vonalak által meghatározott téglalapok területének aránya éppen megadja \(\displaystyle x\) és \(\displaystyle y\), illetve \(\displaystyle u\) és \(\displaystyle v\) arányát:

\(\displaystyle x : y = (2\cdot2a):(12a-2\cdot2a)=4a : 8a = 4:8 = 1:2;\;\; u : v = (2\cdot3a):(12a-2\cdot3a)=6a : 6a = 1:1.\)

Statisztika:

117 dolgozat érkezett.
6 pontot kapott:	82 versenyző.
5 pontot kapott:	14 versenyző.
4 pontot kapott:	5 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	3 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	3 dolgozat.

A KöMaL 2020. februári matematika feladatai