A K. 672. feladat (2020. november)

K. 672. Egy kiskert 16 parcellára van osztva az ábra szerint. Minden egyes parcellába rózsát, tulipánt, margarétát vagy gerberát ültetnek úgy, hogy minden parcellába csak egyféle virág kerüljön és minden sorban, minden oszlopban és minden átlóban lévő négy parcellában minden virágból legyen. Hányféleképpen lehet ezekkel a virágokkal a fenti módon beültetni a kertet? (Két ültetés különböző, ha van olyan parcella, melyben nem ugyanazok a virágok vannak.)

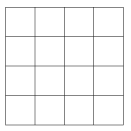
(6 pont)

A beküldési határidő 2020. december 10-én LEJÁRT.

1. megoldás. A kert négy sarokparcellájában négy különböző virág kell, hogy legyen, hiszen párosával egy sorban, oszlopban, illetve átlóban lesznek. A négy virágot jelölje A, B, C és D. Helyezzük el ezeket a sarokparcellákba valamilyen sorrendben. (Huszonnégy sorrend lehetséges, az ábrán egyet látunk.)

Helyezzük el először a A-kat! Mivel az egyik átlóba A már nem kerülhet, így a második sorban a harmadik vagy a negyedik parcellába ültethetjük csak a A-t.

I. Legyen először a harmadikban az A, a többi A helye már adódik.

A harmadik sor második parcellájába C-t kell írni az átló miatt, ekkor a többi C helye is adódik már, és így a többi B és D helye is.

II. Legyen most a második sor negyedik parcellájában az A, a többi A helye már adódik. Helyezzük el a többi C-t! Az BD átlóban kell lennie C-nek, és már csak egy hely volt szabad, így a második sor harmadik parcellája C, a többi C helye már adódik. Az alsó sorból egy B hiányzik, így a többi B helyét, illetve a többi D helyét is egyértelműen megtaláljuk már.

Mivel ehhez az A-B-C-D elhelyezéshez kétféle befejező elrendezést találtunk és az A, B, C és D elhelyezése 24-féle lehet, így összesen 48-féleképpen lehet beültetni a kertet a feltételeknek megfelelően.

2 megoldás. A kert négy sarokparcellájában négy különböző virág kell, legyen, hiszen párosával egy sorban, oszlopban, illetve átlóban lesznek. A négy virágot jelölje A, B, C és D. Helyezzük el ezeket a sarokparcellákba valamilyen sorrendben (huszonnégy sorrend lehetséges). A középső négy mezőt négyféleképpen ültethetjük be.

E négy lehetőség közül kettőt lehet a feltételeknek megfelelően befejezni. (Az első és az utolsó ábra szerint.)

Mivel ehhez az A-B-C-D elhelyezéshez kétféle befejező elrendezést találtunk és az A, B, C és D elhelyezése 24- féle lehet, így összesen 48-féleképpen lehet beültetni a kertet a feltételeknek megfelelően.

Statisztika:

98 dolgozat érkezett.
6 pontot kapott:	Bacsek Emma Borbála, Barta Veronika, Biró Anna, Bóta Bálint, Buday Noémi, Csima Borbála, Dancsák Dénes, Érdi Ferenc Vince, Farkas Zsófia, Fórizs Emma, Görcsös Ákos Attila, Heltovics Lilla, Horváth 221 Zsóka, KrakompergerBence, Kuba Nikoletta, Kurucz Kitti, Mayer Krisztián, Molnár Kristóf, Őszi Nóra, Sándor Eszter, Sebestyén József Tas, Simon Géza, Skrabák Virág, Susán Henrik, Szabó Csenge, Varga 621 Emese .
5 pontot kapott:	Árvai Benedek, Duan Jiayi, Görgényi András Levente, Heim Flóra, Jenei Ákos Zoltán, Kéki Edit, Lajos Luca, Lupkovics Lilla, Markovics Áron, Mészáros Ádám, Pilz Helga, Silye Zoltán, Vesztergombi Júlia.
4 pontot kapott:	11 versenyző.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	8 versenyző.
1 pontot kapott:	15 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2020. novemberi matematika feladatai