A K. 74. feladat (2006. február)

K. 74. Az ábrán kétféle festékesdoboz látható. Anna, Balázs, Csilla és Dalma úgy keverik ki a festéket a tojásfestéshez, hogy becsukott szemmel kétszer egymás után belemártják ecsetjüket valamelyik doboz valamelyik rekeszébe, és az így kapott keverékszínt viszik a tojásra. Anna mindkétszer az első, Balázs mindkétszer a második, Csilla először az első, majd a második, Dalma először a második, majd az első dobozba mártja ecsetjét. Melyikük kapja a legkisebb eséllyel a kék és piros keverékeként adódó lila színt?

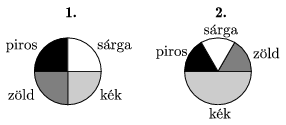
(6 pont)

A beküldési határidő 2006. március 10-én LEJÁRT.

Megoldás: Mind a négyen úgy kaphatnak lilát, ha először a kékbe, utána a pirosba, vagy először a pirosba, utána a kékbe nyúlnak ecsetjükkel. Ha Anna elsőre a kékbe nyúl, ami az estek 1/4-ében fordul elő, akkor másodszorra a pirosba kell nyúlnia, aminek szintén 1/4 az esélye, így lilát 1/16-od valószínűséggel kap, mivel a fordított sorrend esélye is ugyanennyi, összességében 1/8 eséllyel kever ki lilát. Balázs 1/6 eséllyel nyúl elsőre a pirosba, utána 1/2 eséllyel a kékbe, így ennek a valószínűsége 1/12, de a fordított sorrend is jó, így összességében 1/6 az esélye a lila színre. Csilla elsőre 1/4 eséllyel nyúl a pirosba, másodikra 1/2 eséllyel a kékbe, ill. elsőre 1/4 eséllyel a kékbe, másodikra 1/6 eséllyel a pirosba, azaz Csilla esélye a lilára: 1/8+1/24=1/6. Dalma ugyanazt teheti, mint Csilla, csak fordított sorrendben, így neki is 1/6 az esélye. A legkisebb eséllyel tehát Anna kap lilát.

Statisztika:

146 dolgozat érkezett.
6 pontot kapott:	82 versenyző.
5 pontot kapott:	3 versenyző.
4 pontot kapott:	18 versenyző.
3 pontot kapott:	12 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	10 versenyző.
Nem versenyszerű:	6 dolgozat.

A KöMaL 2006. februári matematika feladatai