A K. 770. feladat (2023. május)

K. 770. Hányszor annyi olyan mező van a sakktáblán, amelyről a huszár legalább négy mezőre léphet tovább, mint amelyről nyolc mezőre léphet?

Javasolta: Bíró Bálint (Eger)

(5 pont)

A beküldési határidő 2023. június 12-én LEJÁRT.

1. megoldás. A huszár a sakktáblán L-alakban léphet, az L-alak egyik szélső mezőjéből a másikba (az alábbi ábrán csillaggal jelölve).

Ha a huszár a sakktábla valamelyik sarokmezőjén áll, akkor onnan egy lépésben csak kétféle mezőre léphet, ha pedig egy sarokmező mellett közvetlenül elhelyezkedő szélső mezőn van, akkor csak háromféle lépési lehetősége van. Például az alábbi ábra \(\displaystyle H_1\) jelű sarokmezőjéről indulva a huszár csak az \(\displaystyle X\)-szel jelölt mezőket foglalhatja el, a \(\displaystyle H_2\) jelű mezőről pedig az \(\displaystyle Y\)-nal jelölt három mezőt.

1. ábra

Ha a huszár a sakktábla valamelyik szélső mezőjén áll, de nem sarokmezőn, vagy azzal élben szomszédos mezőn, akkor onnan egy lépésben már négyféle mezőt választhat célpontként. Ezeket a lehetőségeket ábrázoltuk a 2. ábrán, ahol a \(\displaystyle H_3\) mezőről induló huszár a \(\displaystyle Z\)-vel jelölt mezőkre léphet.

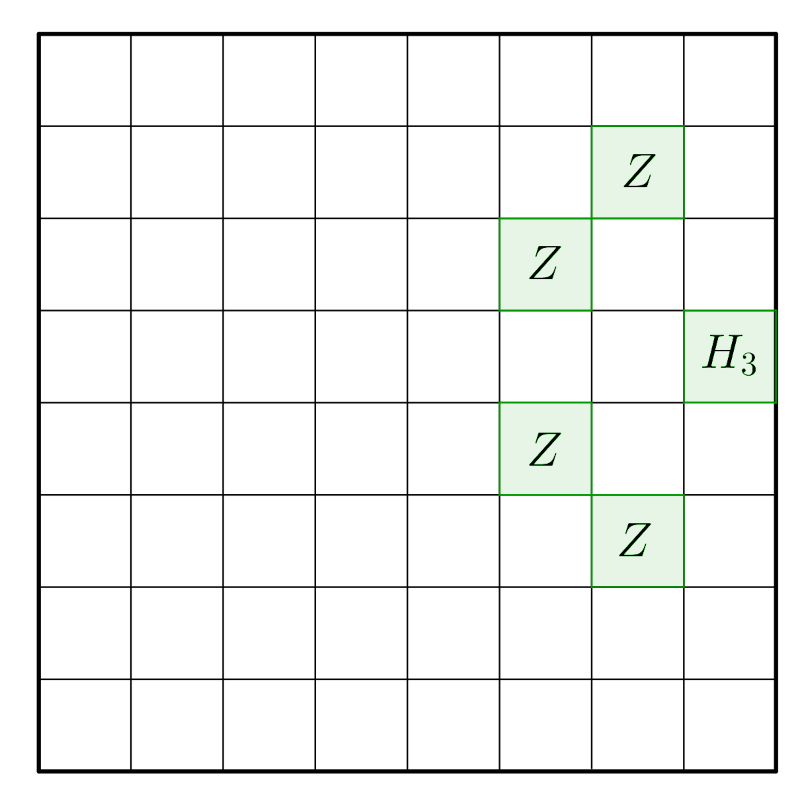
2. ábra

A fentiek alapján nyilvánvaló, hogy a sakktáblának azokról a további mezőiről, amelyek nem a sakktábla szélein helyezkednek el, a huszár egy lépése legalább négyféleképpen valósítható meg. A sarokmezők száma \(\displaystyle 4\), a sarokmezőkkel élben szomszédos mezők száma \(\displaystyle 4\cdot2=8\), ezért azon mezők száma, ahonnan legalább négyféleképpen léphet tovább a huszár, pontosan \(\displaystyle 64-12=52\).

Számoljuk össze most azokat a mezőket, ahonnan legalább \(\displaystyle 8\) mezőre léphet a huszár. Ehhez bejelöljük a sakktábla közepére szimmetrikusan elhelyezkedő \(\displaystyle 6\times6\)-os, illetve \(\displaystyle 4\times4\)-es négyzeteket.

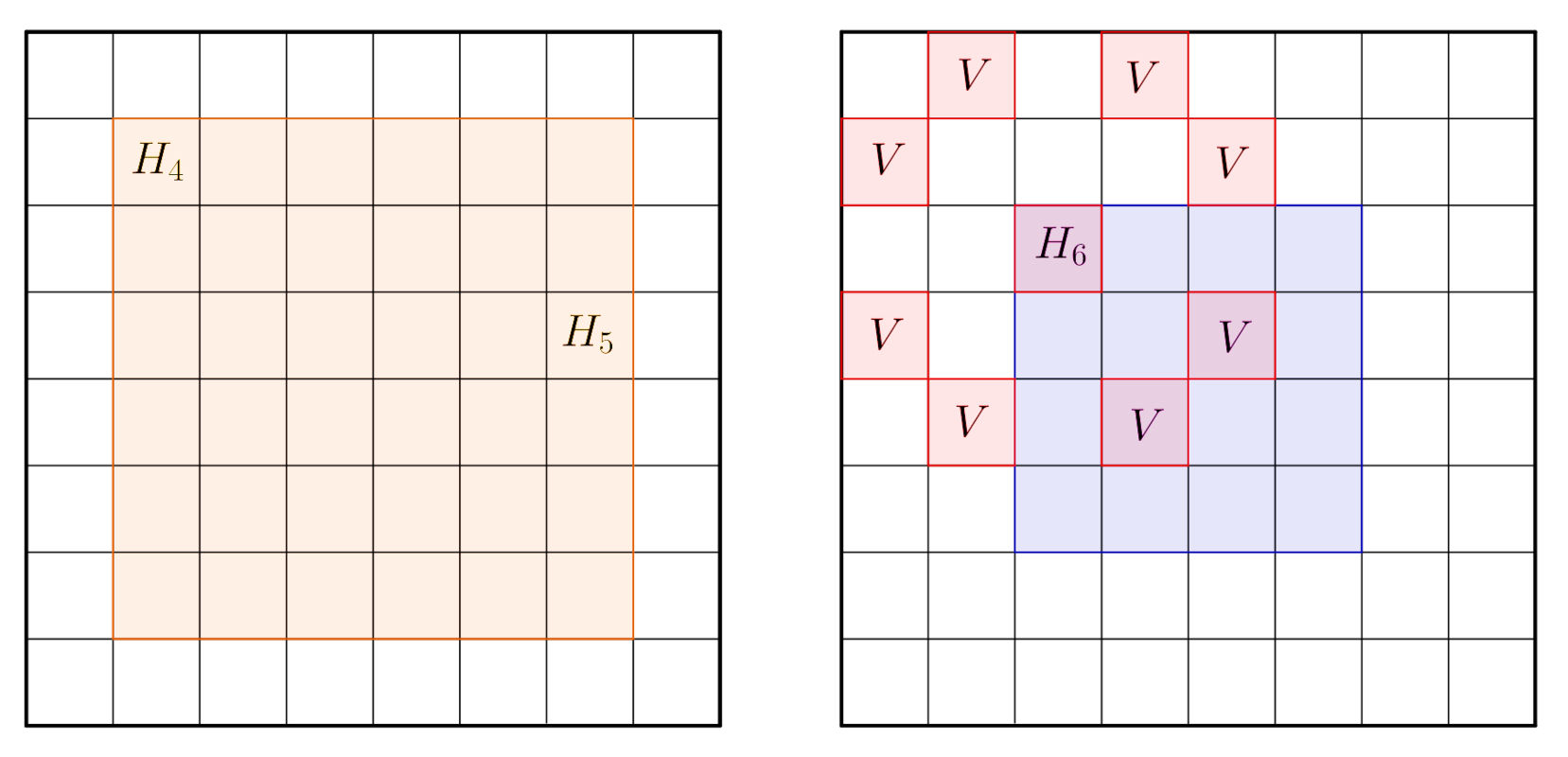
3. ábra

Könnyen látható, hogy a 3. ábra bal oldali \(\displaystyle 6\times6\)-os négyzetének \(\displaystyle H_4\)-gyel jelölt sarokmezőjéről induló huszárnak négyféle választási lehetősége van, míg a \(\displaystyle 6\times6\)-os négyzet egy szélső, de nem sarokmezőjéről, például a \(\displaystyle H_5\) mezőről indulva hatféle. Az ilyen mezőkről tehát a huszár nem léphet legalább nyolcféle mezőre.

A 3. ábra jobb oldali \(\displaystyle 4\times4\)-es négyzetének \(\displaystyle H_6\) sarokmezőjén álló huszár viszont pontosan 8-féle mezőre léphet, ezeket az ábrán \(\displaystyle V\)-vel jelöltük.

Egyszerűen belátható, hogy ennek a \(\displaystyle 4\times4\)-es négyzetnek bármely más mezőjéről induló huszárnak is csak 8-féle választási lehetősége van.

Ez azt jelenti, hogy pontosan \(\displaystyle 16\) olyan mező van (ezek a sakktábla középpontjára szimmetrikus \(\displaystyle 4\times4\)-es négyzeten levő mezők), amelyekből indulva egy huszár egy lépés során 8-féle mező közül választhat, ennél több lehetőséget adó mező a sakktáblán nincs.

A feladat kérdésére tehát az a válasz, hogy a huszár számára a legalább \(\displaystyle 4\), illetve \(\displaystyle 8\) lépési lehetőséget biztosító mezők számának aránya

\(\displaystyle \displaystyle{\frac{52}{16}=\frac{13}{4}}.\)

Tehát a sakktáblán \(\displaystyle \displaystyle{\frac{13}{4}=3,25}\)-szor annyi olyan mező van, amelyről a huszár legalább négy mezőre léphet tovább, mint amelyről nyolc mezőre.

2. megoldás. Mivel két oldalfelező merőlegesére is szimmetrikus, és ezek a merőlegesek nem haladnak át a mezők belső pontjain, így elegendő egy \(\displaystyle 4\times4\)-es sarokdarabon vizsgálni az arányt. A kétféle mezők száma (,,legalább négy", illetve ,,legalább nyolc") ugyanis négyszeres lesz a teljes táblán, mint a kiválasztott \(\displaystyle 4\times4\)-es sarokdarabon, vagyis az arányuk ugyanannyi lesz.

A \(\displaystyle 4\times4\)-es saroknegyed mezői a sakktábla sarkából induló átlójukra szimmetrikusak a lólépések szempontjából (a másik átlóra nem szimmetrikusak), így az eredeti tábla \(\displaystyle 64\) mezője helyett elegendő \(\displaystyle 10\) mezőt megnézni, hány helyre léphetne egy ott álló huszár. Könnyen ellenőrizhető, hogy ebből a tíz mezőből a beleírt számnak megfelelő lépési lehetősége van a huszárnak:

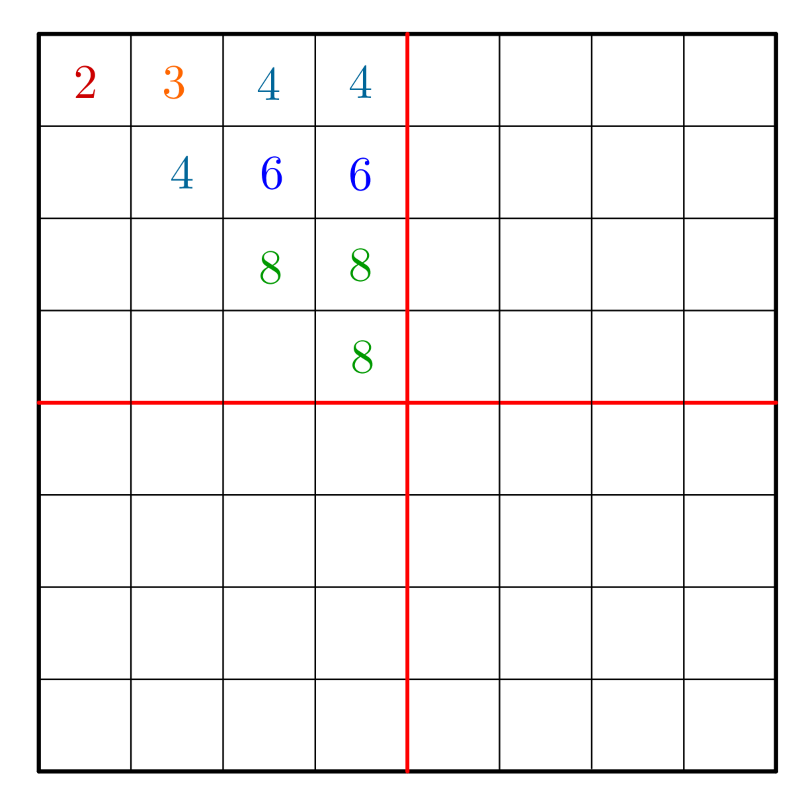
4. ábra

Így a saroknegyedben lévő mezőkről a lépési lehetőségek számai:

5. ábra

Az 5. ábráról leolvasható, hogy a legalább négy lépési lehetőséget jelentő mezők száma \(\displaystyle 13\), a nyolc lehetőséget adó mezők száma pedig \(\displaystyle 4\), vagyis \(\displaystyle \displaystyle{\frac{13}{4}=3,25}\)-szor annyi olyan mező van a sakktáblán, amelyről a huszár legalább négy mezőre léphet tovább, mint amelyről nyolc mezőre.

Statisztika:

32 dolgozat érkezett.
5 pontot kapott:	Bartusková Viktória, Bodor Csanád, Budai Máté, Csikai Anna Alida, Derűs Ádám , Domján István, Horváth Imre, Juhász Noel, Kiss Máté, Kókai Ákos, Kökény Kristóf, Labádi Balázs, Libor Andrea, Ligeti Ábel, Molnár Lili, Móricz Zsombor, Papp Levente, Pulka Gergely Tamás, Sipos Márton, Szabó 926 Bálint, Szabó 926 Bence, Szabó Dániel György, Tajta Sára, Tóth Hanga Katalin, Wolf Erik.
4 pontot kapott:	Hodossy-Takács Ráhel.
3 pontot kapott:	4 versenyző.
1 pontot kapott:	1 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2023. májusi matematika feladatai