 |
A K. 80. feladat (2006. március) |
K. 80. A poliminók a dominók mintájára épülnek fel: kis négyzetekből állnak, melyek mindig teljes oldallal csatlakoznak egymáshoz. Egy P poliminó ,,határoló-számának'' azt a számot nevezzük, ahány különböző módon átfedés nélkül körülhatárolhatjuk a P egybevágó példányaival (minden éléhez csatlakoznia kell egy határoló poliminónak; a poliminót alkotó kis négyzeteknek teljes oldalukkal kell egy másik ilyen négyzethez csatlakozni). Például a kereszt alakzat határoló-száma 2, mert a következő két módon lehet körbehatárolni (a tükrözéssel egymásba vihető körülhatárolások is különbözőnek számítanak).
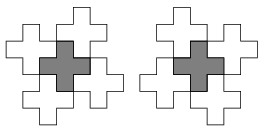
Adjuk meg a 3×3-as (vagyis 9 kis négyzetből álló) négyzet határoló-számát.
(6 pont)
A beküldési határidő 2006. április 10-én LEJÁRT.
Megoldás: Egy 3×3-as négyzet egy oldalának lefedéséhez legfeljebb két 3×3-as négyzet elég. Az első négyzetet 3-féleképpen illeszthetjük az oldalhoz, és ez meghatározza a második helyét (ha kell második). A lefedett oldallal szemközti oldalt hasonlóan 3-féleképpen határolhatjuk, ekkor a két kimaradt oldalhoz már csak egyféleképpen tehetünk hozzá négyzetet. Ez eddig 9 különböző határolás, de ugyanezt elmondhatjuk a másik két oldalpárra is, ez már 18 eset, de azt az esetet, amikor minden oldalt csak egy négyzettel határolunk, kétszer számoltuk, így egyszer le kell vonni. Tehát 17-féleképpen lehet körülhatárolni a 3×3-as négyzetet önmagával.
Megjegyzés: Hasonló módon bizonyítható, hogy az n×n-es négyzet határoló száma n2-1.
Statisztika:
87 dolgozat érkezett. 6 pontot kapott: Bencs 111 Ferenc, Bíró Attila, Botlik Barnabás, Csányi János Dániel, Csere Kálmán, Danyik Dávid, Elhag Feisal, Englert Dávid, Gazdi László, Gévay Gábor, Hajnal Kristóf, Huszár Kristóf, Izsó Dániel, János Júlia Zsófia, Kálló Gábor, Kovács 007 Attila, Kovács Györgyi, Kunos Ádám, Lang Péter, Lantos Tamás, Leskó Lívia, Márki Róbert, Meszlényi Regina, Michael Swift, Nagy 777 Boglárka, Petróczy Dóra Gréta, Pupli Dorottya, Ripszám Réka, Róka Péter, Schönek Barnabás, Seres Dániel, Slezsák Tamás, Szabó 313 Gábor, Szabó 963 Noémi, Szerb Anna, Szikszai Mónika, Szikszay László, Tamási János. 5 pontot kapott: Besnyő Réka, Kovács Sarolta, Kungl 008 Ákos, Murányi Bence, Petrik Laura, Prinz Dániel, Szabó 222 Rita, Toldi Veronika, Trásy Tamás. 4 pontot kapott: 5 versenyző. 3 pontot kapott: 6 versenyző. 2 pontot kapott: 12 versenyző. 1 pontot kapott: 11 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2006. márciusi matematika feladatai
