A K. 90. feladat (2006. szeptember)

K. 90. Az olimpiai ötkarika által meghatározott 9 részbe beírhatjuk az első kilenc pozitív egész számot úgy, hogy minden karikában 14 legyen az összeg. Ezt mutatja az ábra. Keressük meg, hogyan lehet elhelyezni ugyanezt a 9 számot a kilenc részbe úgy, hogy minden karikában 13 legyen az összeg. Keressünk minél több megoldást.

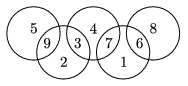
(6 pont)

A beküldési határidő 2006. október 10-én LEJÁRT.

Megoldás: Az öt karika mindegyikében az összeg 13, ez összesen 65, míg az első 9 számjegy összege 45. Tehát a négy metszetben a számok összege 20 kell legyen. Ez, valamint, hogy két számból csak háromféleképpen (9+4=7+6=8+5) lehet a 13-at összerakni, lecsökkentik a lehetőségek számát. Az összes lehetőséget kipróbálva ezt a két megoldást kapjuk:

Statisztika:

270 dolgozat érkezett.
6 pontot kapott:	Bene Gergely, Bognár Barna, Dávid János, Fialowski Melinda, Garamszegi Balázs, Grőger Tímea, Gyebnár Zsófia, Hegedűs Csaba, Kovács 729 Gergely, Kovács Anita, Lajtai Krisztina, Lupsic Balázs, Márkus Rebecca Sheila, Mihálka Éva Zsuzsanna, Németh-Csóka Mihály, Pálinkó Márton, Pasztuhov Anna, Südi Anna, Székely Anna Krisztina, Sziráky Flóra, Tóth 004 Tamás, Tutor Gábor, Welsz Edit.
5 pontot kapott:	Galambos 124 Mónika, Gerlei Klára Zsófia, Tölgyesi Péter.
4 pontot kapott:	7 versenyző.
3 pontot kapott:	41 versenyző.
2 pontot kapott:	75 versenyző.
1 pontot kapott:	107 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2006. szeptemberi matematika feladatai