A P. 4237. feladat (2010. március)

P. 4237. Egy \(\displaystyle m\) tömegű, homogén tömegeloszlású, \(\displaystyle a\) oldalélű kockának olyan pályát készítünk, amelyen csúszásmentesen végiggördülve a kocka középpontja egy vízszintes egyenes mentén mozog (,,négyszögletes kerék''). A pálya ,,tetőpontján'' a kocka középpontjának vízszintes irányú \(\displaystyle v_{0}\) kezdősebességet adunk. A tapadási súrlódás elegendően nagy, így mozgása során a kocka sehol nem csúszik meg.

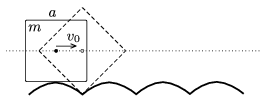
Mekkora lesz a tömegközéppont sebessége, amikor a kocka a pálya legalsó pontját érinti? (A kocka tehetetlenségi nyomatéka a középpontjára vonatkoztatva \(\displaystyle \frac{1}{6}\, ma^2\).)

Közli: Vigh Máté, Pécs

(4 pont)

A beküldési határidő 2010. április 12-én LEJÁRT.

Megoldás. \(\displaystyle \sqrt{5}v_0/2\approx1,\!12v_0.\)

Statisztika:

45 dolgozat érkezett.
4 pontot kapott:	Béres Bertold, Bolgár Dániel, Börcsök Bence, Fekete Károly, Galzó Ákos Ferenc, Jéhn Zoltán, Kánvási Dániel, Kaposvári István, Koncz Gabriella, Kószó Simon, Kungl Ákos Ferenc, Kunsági-Máté Sándor, Láng Hanga, Németh Gábor , Neumer Tamás, Pálovics Péter, Patartics Bálint, Petrács Ervin, Szabó 928 Attila, Szécsényi 136 Andrea, Szélig Áron, Szentgyörgyi 994 Rita, Timkó Réka, Virág Máté.
3 pontot kapott:	Balogh Gábor, Czigány Máté Gábor, Pázmán Koppány.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	9 versenyző.
0 pontot kapott:	6 versenyző.

A KöMaL 2010. márciusi fizika feladatai