 |
A P. 4243. feladat (2010. március) |
P. 4243. \(\displaystyle L=0{,}5\) m hosszú szolenoid (egyenes tekercs) menetszáma \(\displaystyle N=2000\), keresztmetszetének területe \(\displaystyle A=16~\rm cm^2\), belseje \(\displaystyle \mu_{\rm r}=2500\) relatív permittivitású vassal van kitöltve. A tekercsben egy adott pillanatban 100 A/s sebességgel változik az áram erőssége. Mekkora feszültség keletkezik abban a (tekercs közepénél elhelyezkedő) \(\displaystyle 2\ell=20\) cm hosszú egyenes vezetékben, amely
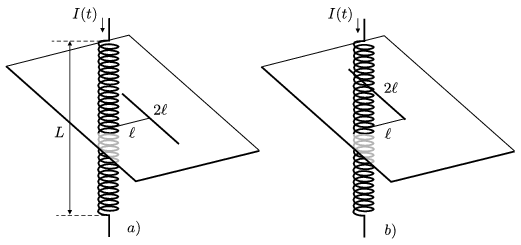
\(\displaystyle a)\) merőleges a tekercs tengelyére, és attól mindkét vége azonos távolságban, a középpontja pedig \(\displaystyle \ell\) távolságban van;
\(\displaystyle b)\) egyik végpontja van \(\displaystyle \ell\) távolságra a tekercs tengelyétől, és iránya az előzővel azonos?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2010. április 12-én LEJÁRT.
Megoldás. \(\displaystyle a)\) \(\displaystyle U_a=\frac{1}{4}\mu_0 \mu_r\frac{NA}{L}\frac{\Delta I}{\Delta t}=0,\!50\) V,
\(\displaystyle b)\) \(\displaystyle U_b=\frac{\arctg 2}{2\pi}\mu_0 \mu_r\frac{NA}{L}\frac{\Delta I}{\Delta t}=0,\!35\) V.
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Balogh Gábor, Béres Bertold, Börcsök Bence, Fonai Dániel, Galzó Ákos Ferenc, Jéhn Zoltán, Kaposvári István, Kószó Simon, Kovács Attila, Kungl Ákos Ferenc, Lájer Márton, Mayer Martin János, Pálovics Péter, Patartics Bálint, Vuchetich Bálint. 4 pontot kapott: Bodosi Eszter, Filep Gábor, Laczkó Zoltán Balázs, Nagy 111 Miklós, Para Attila. 2 pontot kapott: 2 versenyző.
A KöMaL 2010. márciusi fizika feladatai
