 |
A P. 4251. feladat (2010. április) |
P. 4251. Közös pontban felfüggesztettünk két azonos, \(\displaystyle L\) hosszúságú fonálingát. A fonalak végén lévő, azonos tömegű kis golyóknak \(\displaystyle Q\) töltést adunk, aminek következtében a fonalak az ábrán látható módon ágaznak szét.
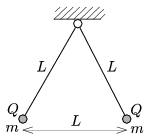
\(\displaystyle a)\) Határozzuk meg a golyók \(\displaystyle m\) tömegét!
\(\displaystyle b)\) Egy másik kísérlet során a jobb oldali golyót ugyanekkora töltésű, de háromszor akkora tömegű golyóra cseréljük ki. Mekkorának kell választani a változatlan tömegű, bal oldali golyó töltését, hogy az egyensúlyi állapotban a golyók távolsága továbbra is \(\displaystyle L\) legyen?
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2010. május 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) \(\displaystyle m=\frac{\sqrt{3}kQ^2}{gL^2}\);
\(\displaystyle b)\) \(\displaystyle Q'=\sqrt{\frac{27}{13}}Q\).
Statisztika:
77 dolgozat érkezett. 5 pontot kapott: Balogh Gábor, Batki Bálint, Benyó Krisztián, Béres Bertold, Bolgár Dániel, Filep Gábor, Fonai Dániel, Fülep Andrea , Galzó Ákos Ferenc, Hartstein Máté, Hegedűs Csaba, Janosov Milán, Jéhn Zoltán, Kaposvári István, Koncz Gabriella, Kovács 444 Áron, Kovács Attila, Kungl Ákos Ferenc, Laczkó Zoltán Balázs, Lőrincz Dóra, Mayer Martin János, Molnár Alexandra, Neumer Tamás, Pálovics Péter, Patartics Bálint, Pázmán Koppány, Pető János, Szabó 928 Attila, Szélig Áron, Szigeti Bertalan György, Tamási Mátyás, Varju 105 Tamás, Vuchetich Bálint, Wirnhardt Bálint. 4 pontot kapott: Kollarics Sándor, Miskó Gergely, Szilágyi 585 Dezső, Várnai Péter. 3 pontot kapott: 10 versenyző. 2 pontot kapott: 8 versenyző. 1 pontot kapott: 20 versenyző. Nem versenyszerű: 1 dolgozat.
A KöMaL 2010. áprilisi fizika feladatai
