 |
A P. 4324. feladat (2011. február) |
P. 4324. Egy  =1 m hosszú fonál egyik végét
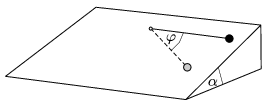
=1 m hosszú fonál egyik végét  =30o hajlásszögű lejtő lapjához rögzítjük. A fonál másik végéhez egy m=1 kg tömegű, pontszerű testet rögzítünk az ábrán látható módon. A testet a fonál kiegyenesített, vízszintes helyzetében kezdősebesség nélkül elengedjük. A lejtő és a test közötti súrlódási együttható
=30o hajlásszögű lejtő lapjához rögzítjük. A fonál másik végéhez egy m=1 kg tömegű, pontszerű testet rögzítünk az ábrán látható módon. A testet a fonál kiegyenesített, vízszintes helyzetében kezdősebesség nélkül elengedjük. A lejtő és a test közötti súrlódási együttható  =0,2.
=0,2.
a) Határozzuk meg a lejtőn lecsúszó test maximális sebességét!
b) Mekkora a fonálban ébredő erő abban a helyzetben, amikor a fonál (először)  =60o-os szöget zár be a kezdeti állapotával?
=60o-os szöget zár be a kezdeti állapotával?
c) A fonál melyik helyzetében maximális a fonálerő?
Közli: Pálfalvi László, Pécs
(5 pont)
A beküldési határidő 2011. március 10-én LEJÁRT.
Megoldás. \(\displaystyle a\)) Ha a test sebessége maximális, akkor az érintőleges gyorsulása épp zérus:
\(\displaystyle mg \sin \alpha \cos \varphi-\mu mg \cos \alpha =0,\)
ebből a maximális sebességnek megfelelő helyzet: \(\displaystyle \varphi=\arccos \left( \frac{\mu}{tg \alpha}\right)\approx 69,\! 7^{\circ}\).
\(\displaystyle b)\) A munkatételből és a Newton-féle mozgásegyenlet sugárirányú komponenséből a fonálerő nagysága egy \(\displaystyle \varphi\) szögű helyzetben:
\(\displaystyle F=(3\sin \varphi \sin \alpha -2\mu \varphi \cos\alpha)mg,\)
így pl. \(\displaystyle \varphi=60^{\circ}\)-ra \(\displaystyle F\approx 9,\! 2\) N.
\(\displaystyle c\)) Az \(\displaystyle F\) erő fenti kifejezéséből deriválással vagy elemi megfontolásokkal megkapható a fonálerő maximumának helye: \(\displaystyle \varphi=\arccos\left( \frac{2\mu}{3 \tg \alpha}\right)\approx 76,\!6 ^{\circ}.\)
Statisztika:
69 dolgozat érkezett. 5 pontot kapott: Ábrahám Attila, Antalicz Balázs, Barta Szilveszter Marcell, Batki Bálint, Béres Bertold, Bojtár Orsika, Filep Gábor, Horváth 721 Klaudia, Jéhn Zoltán, Jenei Márk, Juhász Péter, Koncz Gabriella, Kovács 444 Áron, Kunsági-Máté Sándor, Laczkó Zoltán Balázs, Mázik László, Nagy 111 Miklós, Papp Roland, Park Choong Eun, Pázmán Koppány, Szabó 928 Attila, Tamási Mátyás, Ürge László, Várnai Péter, Zahemszky Péter. 4 pontot kapott: Bolgár Dániel, Herczeg Ferenc, Kollarics Sándor, Maknics András, Pataki Bálint Ármin, Szélig Áron, Szentgyörgyi 994 Rita, Tóth Balázs. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 14 versenyző. 0 pontot kapott: 4 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2011. februári fizika feladatai
