 |
A P. 4388. feladat (2011. november) |
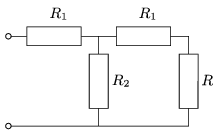
P. 4388. Az ábrán látható áramkörben R1 és R2 ismeretében válasszuk meg R értékét úgy, hogy az áramkör eredő ellenállása
a) ugyancsak R legyen;
b) előírt R0 legyen! (Milyen R0 írható elő?)
Közli: Simon Ferenc, Zalaegerszeg
(5 pont)
A beküldési határidő 2011. december 12-én LEJÁRT.
Megoldás. \(\displaystyle a)\) \(\displaystyle R=\sqrt{R_{1}(R_{1}+2R_{2})}.\)
\(\displaystyle b)\)
\(\displaystyle R=\frac{R_{0}(R_{1}+R_{2})-R_{1}(R_{1}+2R_{2})}{R_{1}+R_{2}-R_{0}},\)
ahol
\(\displaystyle R_{1}+R_{2} \ge R_{0}\ge R_{1}+\frac{R_{1}R_{2}}{R_{1}+R_{2}}.\)
Az egyik határeset a matematikailag ,,helytelen'', de fizikailag megvalósítható, reális lehetőségnek, a végtelen \(\displaystyle R\)-nek (vagyis a szakadásnak) felel meg.
Statisztika:
154 dolgozat érkezett. 5 pontot kapott: 56 versenyző. 4 pontot kapott: 27 versenyző. 3 pontot kapott: 34 versenyző. 2 pontot kapott: 25 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 6 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2011. novemberi fizika feladatai
