A P. 4427. feladat (2012. március)

P. 4427. Egy L hosszúságú vasrudat a két végéhez erősített, hosszúságú fonalak segítségével közös pontban felfüggesztünk. A rudat a fonalak síkjában kicsit kitérítjük.

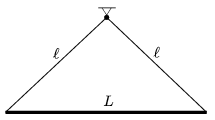
Milyen hosszúságú fonalak esetén lesz a rúd kis lengéseinek periódusideje a lehető legkisebb, és mekkora ebben az esetben a lengésidő?

Közli: Cserti József, Budapest

(5 pont)

A beküldési határidő 2012. április 10-én LEJÁRT.

Megoldás. \(\displaystyle \ell=L/\sqrt{3}\) esetén \(\displaystyle T=T_{\rm min}=2\pi\sqrt{\frac{L}{\sqrt{3}g}}.\)

Statisztika:

48 dolgozat érkezett.
5 pontot kapott:	Antalicz Balázs, Barta Szilveszter Marcell, Bingler Arnold, Bolgár Dániel, Csáky Pál, Csathó Botond, Cseuz Áron, Dinev Georgi, Fehér Zsombor, Filep Gábor, Fonyó Viktória, Horváth Dániel, Janzer Olivér, Jenei Márk, Kollarics Sándor, Koncz Gabriella, Kovács 444 Áron, Laczkó Zoltán Balázs, Lévai 482 Nikolett, Mázik László, Nagy Lajos, Öreg Zsombor, Papp Roland, Sárvári Péter, Seres Imre, Seress Dániel, Simig Dániel, Szabó 928 Attila, Szigeti Bertalan György, Ürge László.
4 pontot kapott:	Büki Máté, Czipó Bence, Juhász Péter, Szélig Áron.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	6 versenyző.

A KöMaL 2012. márciusi fizika feladatai