A P. 4504. feladat (2013. január)

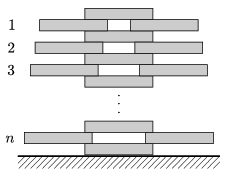
P. 4504. hosszúságú dominókból az ábrán látható szimmetrikus, n emelet magas tornyot építettük. Milyen hosszúak a torony erkélyei, ha mindegyik dominót a lehető legjobban kihúzzuk?

Közli: Vladár Károly, Budapest

(5 pont)

A beküldési határidő 2013. február 11-én LEJÁRT.

Megoldásvázlat. Az ,,erkélyek" kilógó részének hossza:

\(\displaystyle d_1=\frac{2}{3}\ell,\qquad d_2=\frac{5}{6}\ell,\qquad d_3=\frac{8}{9}\ell,\qquad \ldots \qquad d_n=\frac{3n-1}{3n}\ell.\)

Statisztika:

70 dolgozat érkezett.
5 pontot kapott:	Antalicz Balázs, Asztalos Bogdán, Balogh Menyhért, Barta Szilveszter Marcell, Bingler Arnold, Bugár 123 Dávid, Buttinger Milán, Büki Máté, Csáky Pál, Csathó Botond, Csóka József, Czipó Bence, Fehér Zsombor, Fekete Panna, Forrai Botond, Holczer András, Horváth András Levente, Janzer Barnabás, Jenei Márk, Juhász Péter, Kaprinai Balázs, Kasza Bence, Kaszás Bálint, Kollarics Sándor, Kovács 444 Áron, Kovács-Deák Máté, Morvay Bálint, Nárai Ádám, Olexó Tünde, Olosz Balázs, Öreg Botond, Papp Roland, Reitz Angéla, Sal Kristóf, Sárvári Péter, Soós Tamás Sándor, Szabó 928 Attila, Szathmári Balázs, Sztilkovics Milán, Tatár Dániel, Tilk Bence, Trócsányi Péter, Ürge László, Vajda Balázs, Zahemszky Péter, Zarándy Álmos, Zsiros Ádám.
4 pontot kapott:	8 versenyző.
3 pontot kapott:	6 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	4 versenyző.

A KöMaL 2013. januári fizika feladatai