A P. 4588. feladat (2013. december)

P. 4588. Az a oldalélű, m tömegű, homogén tömegeloszlású kockát egy érdes felületű, sík tartóra helyezzük, és az egyik oldaléle mentén egy kicsiny ütközőhöz illesztjük. A tartót fonalakkal felfüggesztjük a kocka tömegközéppontja felett  magasságban (lásd az ábrát), majd a rendszert ingaként bizonyos szöggel óvatosan kitérítjük, és ott elengedjük.

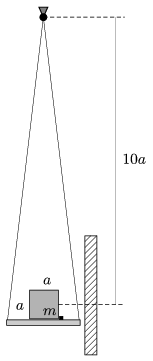
Amikor az inga legmélyebb helyzetébe visszaérkezik, a sík tartó egy nagy tömegű falba ütközik. Mekkora volt a kitérítés szöge, ha a kocka átborul az ütközőn? Az ütközések tökéletesen rugalmatlanok.

(A tartó és a fonalak tömege a kocka tömege mellett elhanyagolható. A kocka tehetetlenségi nyomatéka a középpontján átmenő bármely tengelyre ma²/6.)

Közli: Gnädig Péter, Vácduka

(5 pont)

A beküldési határidő 2014. január 10-én LEJÁRT.

Megoldásvázlat. Az energiamegmaradás törvényéből kiszámíthatjuk a kocka ütközés előtti sebességét, és ebből a kocka perdületét. Az ütközéskor a kockára csak az ütközőnél hat nagy erőlökés, tehát ezen pontjára vonatkozó perdülete megmarad. Ha az ütközés utáni mozgási energiája elegendő a tömegközéppontjának megfelelő megemeléséhez, akkor a kocka átbillen. Ennek az a feltétele, hogy a kitérítés szöge \(\displaystyle \alpha>\alpha_{\rm min}\approx 20^\circ\) legyen.

Statisztika:

34 dolgozat érkezett.
5 pontot kapott:	Balogh Menyhért, Berta Dénes, Blum Balázs, Fehér Zsombor, Fekete Panna.
4 pontot kapott:	Holczer András, Horicsányi Attila, Janzer Barnabás, Olosz Balázs, Trócsányi Péter.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	12 versenyző.

A KöMaL 2013. decemberi fizika feladatai