A P. 4593. feladat (2013. december)

P. 4593. Két részecske a fénysebességhez nagyon közeli (ultrarelativisztikus) sebességgel rugalmasan ütközik. A részecskék ütközés előtti impulzusvektorai az ábrán láthatók. Szerkesszük meg azt a legkisebb szöget, amelyet a szétrepülő részecskék mozgásiránya bezárhat egymással!

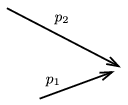
Közli: Vigh Máté, Budapest

(6 pont)

A beküldési határidő 2014. január 10-én LEJÁRT.

Megoldásvázlat. A szétrepülő részecskék impulzusának összege \(\displaystyle \boldsymbol p_1+\boldsymbol p_2\), impulzusnagyságaik összege pedig (az energiamegmaradás miatt) \(\displaystyle \vert \boldsymbol p_1\vert+\vert\boldsymbol p_2\vert\) kell legyen. A részecskék impulzusa egy ellipszis valamely pontját a fókuszokkal összekötő vektorral, illetve annak \(\displaystyle -1\)-szeresével adható meg. A kérdéses \(\displaystyle \alpha\) szög akkor a legkisebb, ha az ellipszis pontja a kistengely valamelyik végpontja, és ekkor \(\displaystyle \cos \frac{\alpha}2=\frac{\vert\boldsymbol p_1+\boldsymbol p_2\vert}{\vert \boldsymbol p_1\vert+\vert\boldsymbol p_2\vert}\). Ez a szög a képlet alapján könnyen megszerkeszthető.

Statisztika:

13 dolgozat érkezett.
6 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Blum Balázs, Csathó Botond, Fehér Zsombor, Forrai Botond, Holczer András, Horicsányi Attila, Juhász Péter, Sal Kristóf, Trócsányi Péter.
4 pontot kapott:	2 versenyző.

A KöMaL 2013. decemberi fizika feladatai