A P. 4692. feladat (2014. december)

P. 4692. Vízszintes, homogén, \(\displaystyle B=0{,}05\) T indukciójú mágneses mezőben egy \(\displaystyle L=20\) cm hosszú, \(\displaystyle A=12~\rm cm^2\) keresztmetszetű, \(\displaystyle N=400\) menetszámú, egyenes tekercs vízszintes síkban foroghat a közepén átmenő függőleges tengely körül. A tekercs tengelye kezdetben merőleges a mágneses indukcióvonalakra, és két végén egy-egy \(\displaystyle D=24\) N/m direkciós erejű, \(\displaystyle \ell_0=20\) cm hosszúságú, nyújtatlan, másik végén rögzített csavarrugóhoz csatlakozik az ábra szerint. A rugók kezdetben merőlegesek az egyenes tekercs tengelyére.

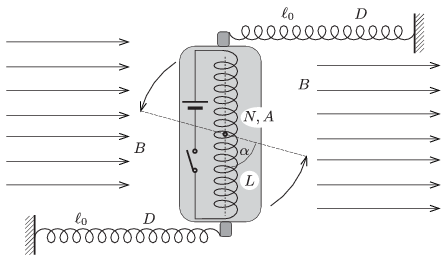
A kapcsoló zárása után a tekercsben áram fog folyni. Mekkora erősségű ez az áram, ha a tekercs \(\displaystyle \alpha=60^\circ\)-os szöggel elfordulva kerül ismét egyensúlyba?

Közli: Holics László, Budapest

(6 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldás: \(\displaystyle I=23{,}3\) A.

Statisztika:

34 dolgozat érkezett.
6 pontot kapott:	Balogh Menyhért, Blum Balázs, Bugár 123 Dávid, Csorba Benjámin, Csurgai-Horváth Bálint, Di Giovanni Márk, Fehér Balázs, Fekete Panna, Forrai Botond, Holczer András, Kasza Bence, Kovács Péter Tamás, Lőrincz Zoltán, Mándoki László, Marosvári Kristóf, Olosz Balázs, Sal Kristóf, Trócsányi Péter.
5 pontot kapott:	Büki Máté, Fülöp Erik, Gróf Tamás, Kaposvári Péter, Körtefái Dóra, Szántó Benedek, Szentivánszki Soma .
4 pontot kapott:	3 versenyző.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2014. decemberi fizika feladatai