A P. 4713. feladat (2015. február)

P. 4713. Függőleges, \(\displaystyle B\) mágneses indukciójú homogén mágneses mezőben lévő fonálon egy \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű, kisméretű golyó függ. A golyónak akkora és olyan irányú sebességet adunk, hogy az vízszintes síkban egyenletes körmozgást végezzen. Egy másik alkalommal úgy állítjuk ugyanolyan sugarú, vízszintes síkú körpályára a golyót, hogy az a mágneses mezőben ellentétes irányban körözzön.

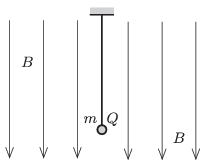
\(\displaystyle a)\) Határozzuk meg a két fonálerő arányát!

\(\displaystyle b)\) Mekkora a szögsebességek nagyságának különbsége a két mozgás során?

Közli: Kotek László, Pécs

(4 pont)

A beküldési határidő 2015. március 10-én LEJÁRT.

Megoldás: \(\displaystyle a)\) A fonálerők aránya 1.

\(\displaystyle b)\) \(\displaystyle \omega_2-\omega_1=\frac{QB}{m}\). (Ezt nevezik az adott mágneses indukcióhoz tartozó ciklotronfrekvenciának.)

Statisztika:

27 dolgozat érkezett.
4 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Csire Roland, Csorba Benjámin, Fehér Balázs, Fekete Panna, Forrai Botond, Fülöp Erik, Iván Balázs, Kasza Bence, Körmöczi Dávid, Körtefái Dóra, Mándoki László, Marosvári Kristóf, Németh Flóra Boróka, Olosz Balázs, Radnai Bálint, Sal Kristóf, Varga-Umbrich Eszter, Varju Ákos, Wiandt Péter.
3 pontot kapott:	Kaposvári Péter.
1 pontot kapott:	1 versenyző.

A KöMaL 2015. februári fizika feladatai