A P. 4744. feladat (2015. május)

P. 4744. A \(\displaystyle B=0{,}02\) tesla indukciójú homogén mágneses térben ugyanazon \(\displaystyle B\)-vonalon két pont \(\displaystyle (X\) és \(\displaystyle Y)\) helyezkedik el egymástól 10 cm távolságra. Az \(\displaystyle X\) ponton egy 800 V feszültséggel felgyorsított elektron halad át, sebessége a \(\displaystyle B\)-vonallal \(\displaystyle \alpha\) szöget zár be. Mekkora lehet az \(\displaystyle \alpha\) szög, ha az elektron az \(\displaystyle Y\) ponton is áthalad?

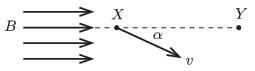
Vermes Miklós (1905-1990) feladata

(5 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás: \(\displaystyle \cos\alpha_N=\frac{3{,}34}{N},\) ahol \(\displaystyle N\ge4\) egész (pl. \(\displaystyle \alpha_4=33{,}5^\circ\); \(\displaystyle \alpha_5=48{,}1^\circ\); \(\displaystyle \alpha_6=56{,}2^\circ\) stb.)

Statisztika:

39 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Bekes Nándor, Berta Dénes, Blum Balázs, Bugár 123 Dávid, Büki Máté, Csathó Botond, Csire Roland, Csorba Benjámin, Fehér Balázs, Fekete Panna, Forrai Botond, Fülöp Erik, Holczer András, Iván Balázs, Jakus Balázs István, Kasza Bence, Körtefái Dóra, Marosvári Kristóf, Molnár 157 Marcell, Németh Flóra Boróka, Olosz Balázs, Öreg Botond, Radnai Bálint, Sal Kristóf, Szentivánszki Soma , Tibay Álmos, Trócsányi Péter.
4 pontot kapott:	Varga-Umbrich Eszter.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	2 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2015. májusi fizika feladatai