A P. 4799. feladat (2016. január)

P. 4799. Az ábrán vázolt áramkörben \(\displaystyle X\) tetszőleges ellenállású lehet.

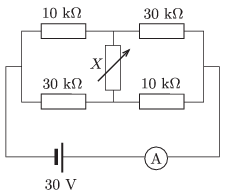
\(\displaystyle a)\) Milyen határok között változhat az árammérő árama?

\(\displaystyle b)\) Mekkora \(\displaystyle X\), ha az árammérő 1,6 mA-t mér?

Versenyfeladat nyomán

(4 pont)

A beküldési határidő 2016. február 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Ha az ellenállásokat kilóohmban, az áramot pedig milliamper egyságekben mérjük, akkor

\(\displaystyle I(X)=1,5+\frac{15}{30+2X}.\)

Ez monoton csökkenő függvény, tehát a legnagyobb (2 mA-es) áramot \(\displaystyle X=0\) (rövidzár) esetén mérhetjük, a legkisebbet (1,5 mA-t) pedig \(\displaystyle X=\infty\) (szakadás) esetén.

\(\displaystyle b)\) A megadott áramerősség \(\displaystyle X=60~\rm k\Omega\) ellenállállásnál mérhető.

Statisztika:

45 dolgozat érkezett.
4 pontot kapott:	Balogh Menyhért, Csorba Benjámin, Csuha Boglárka, Debreczeni Tibor, Fajszi Bulcsú, Farkas Domonkos, Ghada Alshalan, Hajnal Dániel Konrád, Iván Balázs, Kardos Réka, Kárpáti Kristóf, Kluèka Vivien, Krasznai Anna, Mány Bence, Marozsák Tóbiás , Molnár Mátyás, Németh 777 Róbert, Németh Flóra Boróka, Olosz Adél, Pszota Máté, Radnai Bálint, Sallai Krisztina, Szemerédi Levente, Takács Attila, Tóth Adrián, Weisz Pál, Zöllner András.
3 pontot kapott:	Bekes Nándor, Kuchár Zsolt, Paulovics Péter, Tóth Bence.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2016. januári fizika feladatai