 |
A P. 4825. feladat (2016. március) |
P. 4825. Hőszigetelő tartályt hőszigetelő dugattyú oszt egy \(\displaystyle V\) és egy \(\displaystyle 2V\) térfogatú részre. Kezdetben mindkét részben \(\displaystyle T_0=300\) K hőmérsékletű, \(\displaystyle p_0=10^5\) Pa nyomású levegő van. A \(\displaystyle V=2\) liter térfogatú részbe épített \(\displaystyle R=100~\Omega\) ellenállású hődrótos, \(\displaystyle U=230\) V-os melegítőt addig működtetjük, amíg a gázok ,,térfogatot cserélnek'', vagyis az ábra szerinti bal oldali gáz térfogata \(\displaystyle V\)-re, a jobb oldali \(\displaystyle 2V\)-re változik.
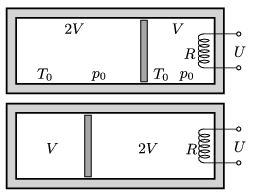
\(\displaystyle a)\) Mekkora lett a hőmérséklet a két tartályban?
\(\displaystyle b)\) Mennyi ideig tartott a folyamat?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2016. április 11-én LEJÁRT.
Megoldás. A bal oldali részben (az adiabatikus állapotváltozás során) kialakuló nyomás:
\(\displaystyle p= 2^{7/5}p_0=2{,}64\,p_0=2{,}64\cdot10^5~\rm Pa.\)
Az egész rendszer belső energiájának megváltozása:
\(\displaystyle \Delta E=\frac52 (p-p_0)\,3V=2460~\rm J.\)
Mivel a hődrótos melegító teljesítménye \(\displaystyle P=U^2/R=529~\)W, a melegítéshez szükséges idő 4,6 másodperc.
A kialakult nyomás és térfogat ismeretében a gáztörvényből kiszámíthatjuk a megváltozott hőmérsékleteket is:
\(\displaystyle T_\text{bal}=\frac{p}{2p_0}T_0=396~\rm K,\)
illetve
\(\displaystyle T_\text{bal}=\frac{2p}{p_0}T_0=1583~\rm K.\)
Statisztika:
59 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Bekes Nándor, Blum Balázs, Csorba Benjámin, Csuha Boglárka, Di Giovanni András, Édes Lili, Elek Péter, Fajszi Bulcsú, Fehér 169 Szilveszter, Fekete Balázs Attila, Forrai Botond, Iván Balázs, Jakus Balázs István, Kasza Bence, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Krasznai Anna, Mány Bence, Marozsák Tóbiás , Molnár Mátyás, Németh 777 Róbert, Németh Flóra Boróka, Olosz Adél, Páhoki Tamás, Pataki 245 Attila, Pázmán Előd, Pszota Máté, Sal Kristóf, Sallai Krisztina, Szentivánszki Soma , Tófalusi Ádám, Tomcsányi Gergely, Varga-Umbrich Eszter, Wiandt Péter, Zöllner András. 4 pontot kapott: Farkas Domonkos, Gémes Antal, Ghada Alshalan, Hornák Bence, Szántó Benedek, Tibay Álmos. 3 pontot kapott: 5 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 6 versenyző.
A KöMaL 2016. márciusi fizika feladatai
