A P. 4827. feladat (2016. március)

P. 4827. Határozzuk meg az ábrán látható áramkörben a főágban és a mellékágakban folyó áramerősségek értékét!

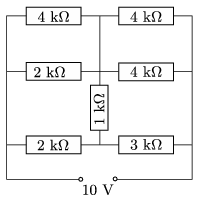
Közli: Simon Péter, Pécs

(4 pont)

A beküldési határidő 2016. április 11-én LEJÁRT.

Megoldás. A két felső ágban lévő 2-2 (párhuzamosan kapcsolt) ellenállás egy \(\displaystyle \tfrac43~\rm k\Omega\)-os és egy \(\displaystyle 2~\rm k\Omega\)-os ellenállással helyettesíthető. Ezek ugyanolyan (\(\displaystyle 2:3\)) arányban osztják a tápfeszültséget, mint az alsó ágban lévő két ellenállás. A középső (\(\displaystyle 1~\rm k\Omega\)-os) ellenállás végpontjai emiatt ekvipotenciálisak, ezen az ellenálláson nem folyik áram. A szélső és a középső pontok közötti potenciálkülönbségből és az ellenállások nagyságából könnyen adódnak az áramerősségek:

Statisztika:

47 dolgozat érkezett.
4 pontot kapott:	Bekes Nándor, Blum Balázs, Bukor Benedek, Csorba Benjámin, Csuha Boglárka, Debreczeni Tibor, Di Giovanni András, Elek Péter, Eper Miklós, Fehér 169 Szilveszter, Fekete Balázs Attila, Gémes Antal, Ghada Alshalan, Iván Balázs, Jakus Balázs István, Kardos Réka, Kasza Bence, Kluèka Vivien, Kormányos Hanna Rebeka, Kovács Péter Tamás, Körmöczi Dávid, Krasznai Anna, Mándoki László, Mány Bence, Molnár Mátyás, Nagy Nándor, Németh Flóra Boróka, Olosz Adél, Paulovics Péter, Pázmán Előd, Sal Kristóf, Sallai Krisztina, Stein Ármin, Szántó Benedek, Szentivánszki Soma , Tófalusi Ádám, Tomcsányi Gergely, Tóth 111 Máté , Varga-Umbrich Eszter, Wiandt Péter.
3 pontot kapott:	Radnai Bálint.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2016. márciusi fizika feladatai