A P. 4837. feladat (2016. április)

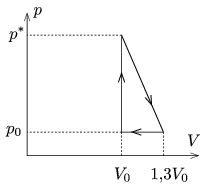
P. 4837. Egy termodinamikai hőerőgép az ábrán látható körfolyamatot végzi. Legalább mekkora \(\displaystyle p^*\) nyomás esetén lesz a gép hatásfoka a legnagyobb, ha a munkavégző közeg állandó tömegű, ideális nemesgáz? Mekkora ez a maximális hatásfok?

(Lásd még Gálfi László Hőfelvétel vagy hőleadás? című cikkét a KöMaL 2009. évi 4. számának 235. oldalán, illetve a honlapunkon: komal.hu/cikkek/cikklista.h.shtml.)

Közli: Radnai Gyula, Budapest

(5 pont)

A beküldési határidő 2016. május 10-én LEJÁRT.

Megoldás. Ha \(\displaystyle p^*\) ,,elegendően nagy'' (ennek pontos jelentését később tisztázzuk), akkor a ferde szakasz meredekségének abszolút értéke (vagyis \(\displaystyle \frac{p^*-p_0}{0{,}3\,V_0}\)) nagyobb, mint az adiabaták meredekségének abszolút értéke. Ilyenkor a gáz a ferde szakaszon biztosan nem vesz fel hőt. Ugyancsak nincs hőfelvétel az izobár összehúzódás során, tehát a gáz hőfelvétele teljes egészében az izochor melegítésnél történik. Ennek nagysága (ciklusonként)

\(\displaystyle Q_\text{fel}=\Delta E=\frac32 \left(p^*-p_0\right) V_0.\)

(Kihasználtuk, hogy az ideális nemesgázok belső energiája \(\displaystyle E=\frac32 pV.\)) Másrészt a ciklusonként végzett munka a \(\displaystyle p-V\) diagramon látható háromszög területével egyenlő:

\(\displaystyle W=\frac12 \left(p^*-p_0\right)\cdot 0{,}3 V_0,\)

és így a gép hatásfoka a vizsgált körülmények között

\(\displaystyle \eta=\frac{W}{Q_\text{fel}}=\frac{0{,}15}{1{,}5}=10\%.\)

Érdekes, hogy ez a hatásfok független \(\displaystyle p^*\)-tól.

Ha \(\displaystyle p^*\) nem elég nagy, akkor a körfolyamat során a ferde szakasz bizonyos részén (vagy esetleg annak egészén) is történik hőfelvétel. Ekkor a termodinamikai hatásfok biztosan kisebb, mint \(\displaystyle 10\%\), hiszen a végzett munka

\(\displaystyle W=\frac12 \left(p^*-p_0\right)\cdot 0{,}3 V_0,\)

a felvett hő pedig

\(\displaystyle Q_\text{fel}> Q_\text{fel}^\text{(izochor)}=\frac32 \left(p^*-p_0\right) V_0,\)

és így a hatásfok

\(\displaystyle \eta=\frac{W}{Q_\text{fel}}<\frac{W}{Q_\text{fel}^\text{(izochor)}}=10\%.\)

Határozzuk meg, milyen nagynak kell lennie \(\displaystyle p^*\)-nak, hogy \(\displaystyle V\) növekedtével az adiabaták kevésbé meredeken csökkenjenek, mint ahogy a derékszögű háromszög átfogója mentén csökken a \(\displaystyle p(V)\) függvény. Az idézett cikk szerint az adiabata meredeksége (nemesgázokra):

\(\displaystyle \frac{\Delta p}{\Delta V}=-\frac53\frac{p}{V}.\)

Így annak feltétele, hogy a ferde szakaszon nincs hőfelvétel:

\(\displaystyle \frac53\frac{p}{V}<\frac{p^*-p_0}{0{,}3V_0}.\)

Ennek az egyenlőtlenségnek a háromszög felső csúcsában is fenn kell állnia:

\(\displaystyle \frac53\frac{p^*}{V_0}<\frac{p^*-p_0}{0{,}3V_0},\)

vagyis ha \(\displaystyle p^*>2p_0\). Könnyű belátni, hogy ha ez teljesül, akkor a ferde szakasz semelyik részén nem történik hőfelvétel.

Összefoglalva az eredményt: a körfolyamat hatásfoka legfeljebb 10 százalék lehet, és ezt az értéket el is éri minden olyan esetben, amikor \(\displaystyle p^*\ge 2p_0\).

Statisztika:

29 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Csorba Benjámin, Csuha Boglárka, Di Giovanni András, Fajszi Bulcsú, Fekete Balázs Attila, Forrai Botond, Krasznai Anna, Németh 777 Róbert, Németh Flóra Boróka, Páhoki Tamás, Sal Kristóf, Szentivánszki Soma , Tomcsányi Gergely, Wiandt Péter.
4 pontot kapott:	Kovács Péter Tamás.
3 pontot kapott:	4 versenyző.
1 pontot kapott:	7 versenyző.

A KöMaL 2016. áprilisi fizika feladatai