 |
A P. 4840. feladat (2016. április) |
P. 4840. Egy derékszögű szögletben, függőleges síkban egy vékony, \(\displaystyle L\) hosszúságú rudat mozgatunk úgy, hogy a rúd vízszintesen mozgó alsó végének sebessége állandó, \(\displaystyle v_0\), a másik vége pedig a mozgás során nem válik el a függőleges faltól. A rúd két végén egy-egy \(\displaystyle Q/2\) töltésű kis gömb található, és az egész rendszer homogén mágneses mezőben van, amelyben a \(\displaystyle \boldsymbol B\) mágneses indukcióvektor vízszintes és az ábra síkjára merőlegesen befelé mutat.
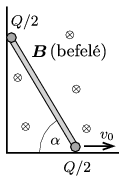
\(\displaystyle a)\) Mekkora nagyságú és milyen irányú erőt fejt ki a mágneses mező a rúdra abban a helyzetben, amikor a rúd \(\displaystyle \alpha\) szöget zár be a vízszintessel?
\(\displaystyle b)\) Határozzuk meg ezt az erőt ugyanebben a helyzetben akkor, amikor nem a rúd végein vannak a töltött gömbök, hanem a rúd középpontjánál helyezkedik el egyetlen, \(\displaystyle Q\) töltésű gömb!
Közli: Kotek László, Pécs
(5 pont)
A beküldési határidő 2016. május 10-én LEJÁRT.
Megoldás. Jelöljük a rúd felső végénél lévő kis gömb (függőlegesen lefelé irányuló) sebességét \(\displaystyle v_1\)-gyel. Ennek nagysága kifejezhető \(\displaystyle v_0\)-lal, hiszen a rúd hossza nem változik, így a két végének ,,rúdirányú'' sebessége egyforma nagy:
\(\displaystyle v_0\cos\alpha=v_1\sin\alpha, \qquad \text{azaz} \qquad v_1=v_0\ctg\alpha.\)
\(\displaystyle a)\) A vízszintesen mozgó kicsiny, töltött gömbre
\(\displaystyle F_0=\frac{Q}{2}v_0 B\)
nagyságú, függőlegesen felfelé irányuló erőt fejt ki a mágneses mező. A függőlegesen lefelé mozgó másik gömbre
\(\displaystyle F_1=\frac{Q}{2}v_1 B=\frac{Q}{2}v_0 B\ctg\alpha\)
nagyságú, vízszintesen jobbra mutató erőt fejt ki a mágneses mező. (Mindkét erő irányának meghatározásánál figyelembe vettük, hogy a mágneses mező az ábra síkjára merőlegesen ,,befelé'' mutat.)

A rúdra ható eredő ,,mágneses erő'' nagysága:
\(\displaystyle \vert {\boldsymbol F}\vert = \sqrt{F_0^2+F_1^2}=\frac{Q}{2}v_0 B\sqrt{1+\ctg^2\alpha}=\frac{Q v_0 B}{2\sin\alpha}.\)
Az eredő erő irányát pl. a vízszintessel bezárt \(\displaystyle \varphi\) szöggel jellemezhetjük:
\(\displaystyle \tg\varphi=\frac{F_0}{F_1}=\tg\alpha, \qquad \text{vagyis}\qquad \varphi=\alpha,\)
tehát az eredő erő vektora a rúd (függőleges vagy vízszintes tengelyre vett) tükörképével megegyező irányú. Másrészt az eredő mágneses erő hatásvonala átmegy az ábrán látható \(\displaystyle P\) ponton. Eszerint a mágneses mező által kifejtett \(\displaystyle \boldsymbol F\) eredő erő a szögletnek a mozgás síkjába eső \(\displaystyle O\) sarokpontjából a rúd \(\displaystyle C\) középpontja felé mutat, és a nagysága a fentebb kiszámított érték.
\(\displaystyle b)\) Ha a rúd középpontjában helyezkedik el \(\displaystyle Q\) nagyságú töltés, ennek vízszintes és függőleges sebességkomponense éppen a fele az a) esetben felírt \(\displaystyle v_0\)-nak és \(\displaystyle v_1\)-nek. Erre a töltésre ható mágneses erő tehát ugyanakkora nagyságú és ugyanolyan irányú lesz, mint a rúd végpontjaiban elhelyezett, \(\displaystyle Q/2\) nagyságú töltésekre ható eredő mágneses erő.
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Asztalos Bogdán, Balogh Menyhért, Bekes Nándor, Büki Máté, Csorba Benjámin, Di Giovanni András, Fehér 169 Szilveszter, Fekete Balázs Attila, Forrai Botond, Ghada Alshalan, Iván Balázs, Jakus Balázs István, Kasza Bence, Kovács Péter Tamás, Körmöczi Dávid, Mány Bence, Marozsák Tóbiás , Németh Flóra Boróka, Olosz Adél, Sal Kristóf, Szántó Benedek, Szentivánszki Soma , Tomcsányi Gergely. 4 pontot kapott: Blum Balázs, Gémes Antal, Krasznai Anna, Makovsky Mihály, Nagy 555 Botond, Németh 777 Róbert, Páhoki Tamás, Tófalusi Ádám. 3 pontot kapott: 3 versenyző.
A KöMaL 2016. áprilisi fizika feladatai
