A P. 4842. feladat (2016. április)

P. 4842. Egy átlátszatlan lapon kicsiny lyukak vannak az ábrán látható szabályos hatszögrács elrendezésben. A lapot monokromatikus, \(\displaystyle \lambda\) hullámhosszúságú lézerfénnyel világítjuk meg merőlegesen.

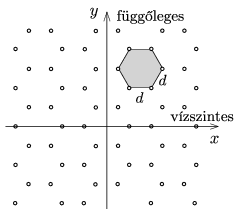
Milyen elhajlási képet figyelhetünk meg a rácstól \(\displaystyle L\) távolságra elhelyezett ernyőn, ha a rácsállandó \(\displaystyle d\)? Mit mondhatunk az intenzitáscsúcsok egymáshoz viszonyított fényességéről? (Feltételezhetjük, hogy \(\displaystyle L\gg d \gg \lambda\).)

(A megoldáshoz segítséget nyújthat a 2005. évi Eötvös-verseny 3. feladatának megoldása, lásd a KöMaL 2006. évi 3. számának 168. oldalán, illetve a honlapunkon: komal.hu/cikkek/cikklista.h.shtml.)

Közli: Vigh Máté, Budapest

(6 pont)

A beküldési határidő 2016. május 10-én LEJÁRT.

Megoldás. A Huygens–Fresnel-elv szerint a lyukak mindegyikéből azonos fázisú és a lyuk területével arányos amplitúdójú gömbhullám indul ki. Ezen hullámok fázishelyes összege adja meg az eredő hullámot, aminek az amplitúdónégyzetével arányos intenzitású elhajlási kép alakul ki az ernyőn.

Ha egy \(\displaystyle d\) rácsállandójú, szabályos háromszögekből álló rácsunk lenne, az elhajlási kép (az idézett cikkben leírtak szerint) egy olyan háromszögrács, amely \(\displaystyle 90^\circ\)-kal elforgatott helyzetű az eredeti rácshoz képest, és szabályos háromszögeinek oldalhossza \(\displaystyle D=\frac{2L\lambda}{\sqrt{3}d}.\)

A feladatban szereplő hatszögrács felfogható úgy is, mint egy \(\displaystyle d\) rácsállandójú háromszögrács és egy \(\displaystyle \sqrt{3}d\) rácsállandójú másik, \(\displaystyle 90^\circ\)-kal elforgatott helyzetű rács különbsége (1. ábra). Ha a ritkább rács (aminek rácspontjait a hatszögek középpontjai alkotják) minden pontjából jövő hullámot levonjuk a sűrűbb háromszögrács hullámaiból, a maradék éppen a feladatban szereplő hatszögrács elhajlási képét adja meg.

1. ábra

A sűrűbb háromszögrács önmagában egy \(\displaystyle D=\frac{2L\lambda}{\sqrt{3}d}\) rácsállandójú, az eredeti rácshoz képest \(\displaystyle 90^\circ\)-kal elforgatott elhajlási képet hoz létre az ernyőn. A ritkább rács elhajlási képe is ilyen jellegű lenne (ha csak önmagában okozná azt), de annak rácsállandója \(\displaystyle D'=\sqrt{3}=\frac{2L\lambda}{d}\), az intenzitása pedig \(\displaystyle 3^2=9\)-szer kisebb lenne. Ez utóbbi faktor onnan származik, hogy a ritkább rácsnak adott területen 3-szor kevesebb pontja van, mint a sűrűbb rácsnak, tehát a belőle kiinduló hullámok eredő amplitúdója 3-szor kisebb, mint a sűrűbb rács esetében.

2. ábra

A két elhajlási kép ,,eredőjét'', vagyis a feladatban szereplő hatszögrács által létrehozott képet a két alrács képének szuperponálásával kapjuk meg (2. ábra). Ez egy olyan hatszögrács lesz, amelyben a hatszögek középpontjában az intenzitás 4-szer erősebb, mint a hatszögek csúcspontjaiban.

Statisztika:

6 dolgozat érkezett.
6 pontot kapott:	Ghada Alshalan, Kovács Péter Tamás.
5 pontot kapott:	Büki Máté.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. áprilisi fizika feladatai