A P. 4846. feladat (2016. május)

P. 4846. Homogén lemezből egyenlő oldalú háromszöget vágunk ki. Ezt kerületének valamely \(\displaystyle P\) pontjában felfüggesztjük. A \(\displaystyle P\) pont és az egyik csúcs távolsága a háromszög oldalhosszának \(\displaystyle x\)-szerese.

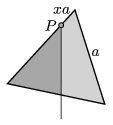
A felfüggesztési ponton átmenő függőleges egyenes a háromszöget két részre osztja; milyen arányban van egymáshoz e két rész tömege? Mikor vesz fel a két tömeg aránya szélsőértéket, és mekkora ezen szélsőérték?

Strasszer V. Benő (1884-1966) feladata

(5 pont)

A beküldési határidő 2016. június 10-én LEJÁRT.

Megoldás. A lemez homogén, emiatt a tömegek aránya helyett vizsgálhatjuk a megfelelő területek arányát. A háromszög \(\displaystyle S\) súlypontja rajta fekszik a \(\displaystyle P\) ponton áthaladó függőleges egyenesen. A kérdés tehát az, hogy a \(\displaystyle PS\) egyenes milyen területarányban osztja két részre a szabályos háromszöget (1. ábra).

1. ábra

Az \(\displaystyle R(x)=\frac{T_1}{T_2}\) függvény \(\displaystyle x=0\) és \(\displaystyle x=\tfrac{1}{2}\) esetén nyilván 1, hiszen ekkor a \(\displaystyle PS\) egyenes a háromszög egyik szimmetriatengelye (szögfelezője). Megmutatjuk, hogy \(\displaystyle 0<x<\tfrac{1}{2}\) esetén \(\displaystyle R>1\), és a maximális értékét \(\displaystyle x=\tfrac{1}{3}\)-nál éri el: \(\displaystyle R(\tfrac{1}{3})=\tfrac{5}{4}\).

Induljunk ki az \(\displaystyle x=0\) helyzetből, és fokozatosan növeljük \(\displaystyle x\) értékét, vagyis távolítsuk a \(\displaystyle P\) pontot a hozzá közelebbi csúcsponttól egy közeli \(\displaystyle P'\) pontig (2. ábra). Ezáltal a \(\displaystyle T_1\) terület megnő az ábrán látható \(\displaystyle \Delta T_2-\Delta T_1\) értékkel, a \(\displaystyle T_2\) terület pedig ugyanennyivel lecsökken.

2. ábra

Mindaddig, amíg \(\displaystyle \ell_1>\ell_2\), a területek kicsiny megváltozására fennáll \(\displaystyle \Delta T_2>\Delta T_1\), vagyis a \(\displaystyle T_1\) terület ténylegesen növekszik, \(\displaystyle T_2\) pedig ténylegesen csökken, az \(\displaystyle R(x)\) arány tehát nagyobbá válik. (A megfontolásunk során a kicsiny háromszögek területét kicsiny körcikkekkel közelítettük, melyek területe \(\displaystyle \ell_1\) és \(\displaystyle \ell_2\) négyzetével arányos.)

Mindez addig érvényes, amíg el nem érjük az \(\displaystyle \ell_1=\ell_2\) helyzetet. Ez akkor teljesül, amikor \(\displaystyle PS\) párhuzamossá válik a háromszög \(\displaystyle AB\) oldalával (3. ábra). Mivel a háromszög súlypontja \(\displaystyle 2:1\) arányban osztja a súlyvonalakat, \(\displaystyle AP=\tfrac13 AC\), vagyis \(\displaystyle x=\tfrac13\), és a \(\displaystyle PQC\) háromszög \(\displaystyle T_2\) területe \(\displaystyle \tfrac{4}{9}\)-ede a teljes \(\displaystyle ABC\) háromszög \(\displaystyle T_1+T_2\) területének, azaz \(\displaystyle R\left(\tfrac13\right)=\tfrac54\).

3. ábra

Ha \(\displaystyle x\)-et tovább növeljük egészen \(\displaystyle \tfrac12\)-ig, \(\displaystyle \ell_1<\ell_2\) miatt \(\displaystyle R(x)\) monoton csökken, és végül eléri az \(\displaystyle R\left(\tfrac12\right)=1\) minimális értékét.

A két tömeg aránya (vagyis a két terület aránya) az

\(\displaystyle f(x)=\frac{1-x-x^2}{1-2x+x^2}\)

függvénnyel adható meg. Ennek a függvénynek a szélsőértékét (mint az a függvény grafikus ábrázolásából, vagy a deriváltjának vizsgálatból kiderül) \(\displaystyle x=1/3\)-nál találjuk, és a szélsőérték nagysága \(\displaystyle 5/4\).

Statisztika:

29 dolgozat érkezett.
5 pontot kapott:	Balogh Menyhért, Bekes Nándor, Bukor Benedek, Di Giovanni András, Édes Lili, Elek Péter, Fehér 169 Szilveszter, Ghada Alshalan, Jakus Balázs István, Kasza Bence, Kluèka Vivien, Marozsák Tóbiás , Molnár Mátyás, Németh 777 Róbert, Németh Flóra Boróka, Olosz Adél, Páhoki Tamás, Póta Balázs, Pszota Máté, Sal Kristóf, Tomcsányi Gergely, Varga-Umbrich Eszter, Wiandt Péter, Zöllner András.
3 pontot kapott:	2 versenyző.
2 pontot kapott:	1 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2016. májusi fizika feladatai