A P. 4849. feladat (2016. május)

P. 4849. Könnyen gördülő kiskocsira rögzített félgömb alakú, \(\displaystyle R=0{,}3\) m sugarú tartály és a kocsi össztömege \(\displaystyle M=2\) kg. Kezdetben egy, a tartály peremével érintkező, \(\displaystyle m=1\) kg tömegű, pontszerűnek tekinthető testet tartunk, majd nyugalomból elengedjük.

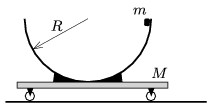
\(\displaystyle a)\) Mekkora a kis test és a kiskocsi sebességének nagysága és iránya akkor, amikor a lecsúszó test \(\displaystyle h=R/2\) értékkel lesüllyedt?

\(\displaystyle b)\) Mekkora a kis test talajhoz rögzített koordináta-rendszerbeli pályájának görbületi sugara, amikor a legmélyebbre kerül?

(A súrlódás mindenütt elhanyagolhatóan kicsi.)

Közli: Holics László, Budapest

(5 pont)

A beküldési határidő 2016. június 10-én LEJÁRT.

Megoldás. \(\displaystyle a)\) Jelöljük a kiskocsi sebességét \(\displaystyle V\)-vel, a lecsúszó test kiskocsihoz viszonyított sebességének nagyságát pedig \(\displaystyle u\)-val. A kérdéses pillanatban a kis test sebessége vízszintes irányban

\(\displaystyle v_x=V-\frac{1}{2}u,\)

függőlegesen pedig

\(\displaystyle v_y=u\frac{\sqrt{3}}{2}.\)

(Kihasználtuk, hogy az \(\displaystyle R/2\) süllyedéshez tartozó helyzetben a kis testhez húzott sugár \(\displaystyle 30^\circ\)-os szöget zár be a vízszintessel.)

A külső erők eredőjének nincs vízszintes irányú összetevője, emiatt a rendszer \(\displaystyle x\) irányú impulzusa megmarad:

\(\displaystyle MV+m\left(V-\frac{1}{2}u\right)=0,\)

így (\(\displaystyle M=2m\) felhasználásával)

\(\displaystyle V=\frac{1}{6}u.\)

Másrészt az energiamegmaradás törvénye szerint

\(\displaystyle \frac{1}{2}m\left(v_x^2+v_y^2 \right) +\frac{1}{2}M V^2=mg\frac{R}{2},\)

ahonnan

\(\displaystyle u=\sqrt{\frac{12}{11}Rg}=1{,}79~\frac{\rm m}{\rm s}; \qquad V=\sqrt{\frac{1}{33}Rg}=0{,}30~\frac{\rm m}{\rm s}\)

következik. Ennek megfelelően

\(\displaystyle v_x=-0{,}60~\frac{\rm m}{\rm s}; \qquad v_y=1{,}55~\frac{\rm m}{\rm s},\)

vagyis a kis test sebességének nagysága

\(\displaystyle \vert \boldsymbol v \vert=\sqrt{v_x^2+v_y^2}=1{,}66~\frac{\rm m}{\rm s},\)

és az iránya \(\displaystyle \varphi=\text{arctg} \frac{v_y}{v_x}\approx 69^\circ\)-os szöget zár be a vízszintessel.

\(\displaystyle b)\) A pálya legalsó pontjánál a fentebb számolt mennyiségek így alakulnak:

\(\displaystyle u= \sqrt{3Rg},\qquad V=\frac{1}{3}u,\qquad v_x=-\frac{2}{3}u, \qquad v_y=0.\)

A kiskocsi gyorsulása a kérdéses pillanatban nulla, így a hozzá rögzített vonatkoztatási rendszer (ebben a pillanatban) inerciarendszernek tekinthető. A test mozgásegyenlete:

\(\displaystyle N-mg = m\frac{u^2}{R},\)

hiszen ebben a rendszerben a kis test \(\displaystyle R\) sugarú körpályán \(\displaystyle u\) sebességgel halad. (\(\displaystyle N\) a kocsi által kifejtett, függőlegesen felfelé mutató kényszererő.)

A talajhoz rögzített koordináta-rendszerben a kis test \(\displaystyle v_x=-\frac{2}{3}u\) pillanatnyi sebességgel mozog, pályájának görbületi sugara a pálya legalsó pontjában (jelöljük ezt \(\displaystyle \varrho\)-val) a keresett mennyiség. A mozgásegyenlet most:

\(\displaystyle N-mg=\frac{v_x^2}{\varrho},\)

ahol \(\displaystyle N\) ugyanakkora, mint amit a másik vonatkoztatási rendszerben kiszámítottunk. A két egyenlet összevetéséből a

\(\displaystyle \varrho=\frac{v_x^2}{u^2}R=\frac{4}{9}R=0{,}133~\rm m \)

eredményt kapjuk.

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Asztalos Bogdán, Balogh Menyhért, Bartók Imre, Büki Máté, Csorba Benjámin, Csuha Boglárka, Di Giovanni András, Fehér 169 Szilveszter, Fekete Balázs Attila, Forrai Botond, Ghada Alshalan, Iván Balázs, Jakus Balázs István, Kluèka Vivien, Kovács Péter Tamás, Krasznai Anna, Marozsák Tóbiás , Molnár Mátyás, Olosz Adél, Páhoki Tamás, Pázmán Előd, Póta Balázs, Sal Kristóf, Szentivánszki Soma , Tófalusi Ádám.
4 pontot kapott:	Bekes Nándor, Berke Martin, Kasza Bence, Makovsky Mihály, Nagy 555 Botond, Németh 777 Róbert.
3 pontot kapott:	5 versenyző.
2 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2016. májusi fizika feladatai