 |
A P. 4887. feladat (2016. december) |
P. 4887. Egy \(\displaystyle f\) fókusztávolságú homorú tükör optikai tengelyén, tőle \(\displaystyle d\) távolságban, az optikai tengelyre merőlegesen, a homorú tükörrel szemben egy síktükör van. Az optikai tengelyen hová helyezzük a pontszerűnek tekinthető \(\displaystyle T\) fényforrást, hogy az abból induló fénysugarak a homorú tükörről, majd a síktükörről visszaverődve ugyanúgy a fényforrás helyén alkossanak képet, mint a síktükörről, majd a homorú tükörről visszaverődő fénysugarak? Milyen feltétel teljesülése esetén lehetséges ez?
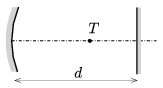
Közli: Zsigri Ferenc, Budapest
(4 pont)
A beküldési határidő 2017. január 10-én LEJÁRT.
Megoldás. Ha egy alkalmas helyen lévő fényforrásról először a homorú tükörről, majd pedig a síktükörről visszaverődő fénysugarak éppen a fényforráshoz jutnak vissza, akkor (a sugármenetek megfordíthatósága miatt) a fordított sorrendben tükröződő fénysugarak is ugyanott fókuszálódnak, ugyanott alkotnak képet. A két feltétel közül tehát elegendő csak az egyiket vizsgálnunk.
Ha a fényforrás a síktükörtől \(\displaystyle x\) távolságban helyezkedik el, akkor a (látszólagos) képe a síktükör túlsó oldalán, a homorú tükörtől \(\displaystyle d+x\) távolságban lesz. A gömbtükör akkor alkot erről a virtuális képről \(\displaystyle d-x\) távolságban valódi képet, ha fennáll
\(\displaystyle \frac{1}{d+x}+\frac{1}{d-x}=\frac{1}{f},\)
vagyis
\(\displaystyle x=\sqrt{d(d-2f)}.\)
Látható, hogy a feladatnak csak \(\displaystyle d\ge 2f\) esetén van megoldása.
Statisztika:
37 dolgozat érkezett. 4 pontot kapott: Bekes Nándor, Bukor Benedek, Debreczeni Tibor, Elek Péter, Faisal Fahad AlSallom, Fajszi Bulcsú, Fekete Balázs Attila, Gulácsi Máté, Jakus Balázs István, Krasznai Anna, Markó Gábor, Marozsák Tóbiás , Molnár Mátyás, Nagy 555 Botond, Németh 123 Balázs, Németh 777 Róbert, Nyerges Dóra, Olosz Adél, Ónodi Gergely, Póta Balázs, Sal Dávid, Szentivánszki Soma , Tófalusi Ádám, Turcsányi Ádám, Varga-Umbrich Eszter, Zöllner András. 3 pontot kapott: Illyés András, Iván Balázs, Molnár Bálint. 2 pontot kapott: 6 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. decemberi fizika feladatai
