 |
A P. 4890. feladat (2016. december) |
P. 4890. Vákuumban függőlegesen felfelé mutató, \(\displaystyle E=6\cdot 10^4\) V/m térerősségű, homogén elektromos mező egy pontjából lefelé, a függőlegessel \(\displaystyle \varphi=30^\circ\)-os szöget bezáró irányban \(\displaystyle v_0= 2\) m/s sebességgel indítunk egy \(\displaystyle m=1\) g tömegű, \(\displaystyle Q=2\cdot 10^{-7}\) C töltésű, pontszerű testet.
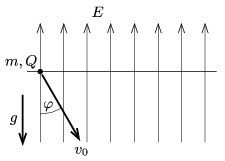
\(\displaystyle a)\) Maximálisan milyen mélyre kerül az eldobás szintjétől mérve?
\(\displaystyle b)\) Mennyi idő alatt éri el a legalsó helyzetet?
\(\displaystyle c)\) Milyen távol lesz a kiindulási ponttól az indulástól számított \(\displaystyle t=1{,}8\) s múlva?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2017. január 10-én LEJÁRT.
Megoldás. A testre függőlegesen felfelé \(\displaystyle QE-mg\) nagyságú erő hat, ez éppen akkora, mintha a nehézségi gyorsulás felfelé mutatna és
\(\displaystyle g'=\frac{QE}{m}-g=2{,}19~\frac{\rm m}{\rm s^2}\)
nagyságú lenne. Ebben a módosult ,,gravitációs térben'' a test a ferde hajítás törvényei szerint mozog.
\(\displaystyle a)\) A kezdősebesség függőleges komponense
\(\displaystyle v_1=v_0\,\cos\varphi=1{,}73~\frac{\rm m}{\rm s}.\)
A test legnagyobb lesüllyedése az indítás szintje alá:
\(\displaystyle h=\frac{v_1^2}{2g'}=0{,}6871~\rm m.\)
\(\displaystyle b)\) A pálya legmélyebb pontját
\(\displaystyle T=\frac{v_1}{g'}=0{,}79~\rm s\)
alatt éri el a test.
\(\displaystyle c)\) A megadott \(\displaystyle t\) idő alatt a test függőleges irányban \(\displaystyle y=\frac{g'}{2}t^2-v_1t= 0{,}43~\rm m\)-t, vízszintes irányban pedig (\(\displaystyle v_2=v_1\sin\varphi=1~\)m/s sebességű egyenletes mozgással) \(\displaystyle x=1{,}8~\)m-t mozdul el. A kiindulási ponttól való távolság ebben a pillanatban \(\displaystyle d=\sqrt{x^2+y^2}=1{,}85~\rm m\) lesz.
Statisztika:
101 dolgozat érkezett. 5 pontot kapott: 64 versenyző. 4 pontot kapott: 22 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 3 dolgozat.
A KöMaL 2016. decemberi fizika feladatai
