A P. 4909. feladat (2017. február)

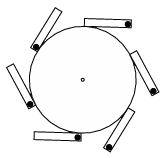
P. 4909. Vízszintes tengelyű kerék kerülete mentén 6 cső helyezkedik el az ábra szerint. Mindegyik csőben nehéz ólomgolyó van. Jobb oldalon a golyók a cső végén, a tengelytől messze, bal oldalon a golyók a cső elején, a tengelyhez közelebb helyezkednek el. Magyarázzuk meg, miért nem lesz örökmozgó (perpetuum mobile) ez a szerkezet!

Vermes Miklós (1905–1990) feladata

(5 pont)

A beküldési határidő 2017. március 10-én LEJÁRT.

Megoldás. A rendszer tömegközéppontjának \(\displaystyle h\) magassága az elfordulás \(\displaystyle \varphi\) szögének függvényében periodikusan változik:

\(\displaystyle h(\varphi+60^\circ)=h(\varphi).\)

Ugyanez érvényes a rendszer helyzeti energiájára is.

Bizonyos helyzetekben az energia az elfordulás függvényében csökken, ezen helyzetekből a kerék ,,magától'' megindul. A periodicitás miatt más helyzetekben az energia ,,lokálisan növekvő'' függvénnyel jellemezhető, ezen helyekről indítva tehát csak munkavégzéssel lehet tovább fordítani a kereket.

Ha a csökkenő helyzeti energiájú szakaszokon a kerék ,,lendületet'' szerez (valójában perdületre tesz szert), akkor ez a lendület a helyzeti energia növekedésével járó szakaszokon lecsökken, és – az egyéb súrlódási veszteségek miatt – a kerék megáll.

Statisztika:

25 dolgozat érkezett.
5 pontot kapott:	Debreczeni Tibor, Fehér 169 Szilveszter, Kántor Bence, Marozsák Tóbiás , Molnár Mátyás, Németh 123 Balázs, Németh 777 Róbert, Olosz Adél, Páhoki Tamás, Póta Balázs.
4 pontot kapott:	Nagy 555 Botond, Varga-Umbrich Eszter.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	11 versenyző.

A KöMaL 2017. februári fizika feladatai