 |
A P. 4913. feladat (2017. február) |
P. 4913. Vékony, elhanyagolható tömegű, \(\displaystyle \ell=20\) cm hosszú fonálra függesztett, \(\displaystyle m=0{,}3\) g tömegű, \(\displaystyle Q =2\cdot 10^{-7}\) C töltésű, kis méretű golyó fonalát a vízszintesig kitérítjük, majd kezdősebesség nélkül elengedjük.
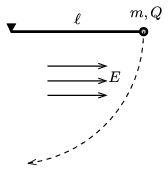
\(\displaystyle a)\) Mekkora lesz a golyó legnagyobb sebessége, ha az egész inga vízszintes, \(\displaystyle E=10^4\) N/C térerősségű, homogén elektromos mezőben van?
\(\displaystyle b)\) Mekkora szöget zár be a függőlegessel a fonál a másik szélső helyzetében?
(A légellenállás elhanyagolható.)
Közli: Holics László, Budapest
(4 pont)
A beküldési határidő 2017. március 10-én LEJÁRT.
Megoldás. A golyóra \(\displaystyle mg=2{,}94\cdot10^{-3}~\)N nagyságú, függőleges irányú erő és \(\displaystyle QE=2{,}0\cdot10^{-3}~\)N nagyságú, vízszintes irányú erő hat. Ez ugyanakkora, mintha a golyó
\(\displaystyle g'= \sqrt{g^2+\left(\frac{QE}{m}\right)}=11{,}86~\frac{\rm m}{\rm s^2} \)
nagyságú, a függőlegessel \(\displaystyle \varphi=\arctg \frac{EQ}{mg}=34{,}2^\circ\)-os szöget bezáró ,,nehézségi gyorsulású'' gravitációs térben mozogna.
Innen számítható, hogy a legnagyobb sebesség 1,4 m/s, és a másik szélső helyzetben a fonál a függőlegessel kb. 22 fokos szöget zár be.
Statisztika:
64 dolgozat érkezett. 4 pontot kapott: Balaskó Dominik, Bartók Imre, Bukor Benedek, Csire Roland, Csóka987 Benedek, Édes Lili, Fehér 169 Szilveszter, Fekete Balázs Attila, Hajnal Dániel Konrád, Illés Gergely, Klučka Vivien, Kolontári Péter, Kozák András, Krasznai Anna, Kürti Zoltán, Magyar Róbert Attila, Markó Gábor, Molnár Mátyás, Morvai Orsolya, Nagy 555 Botond, Olosz Adél, Páhoki Tamás, Pataki 245 Attila, Póta Balázs, Sal Dávid, Tóth 111 Máté , Tóth 420 Péter, Tóth Bence, Varga-Umbrich Eszter, Weisz Máté, Zöllner András, Zsombó István. 3 pontot kapott: Ardai István Tamás, Bekes Nándor, Bíró Dániel, Csuha Boglárka, Elek Péter, Fazakas Réka, Fehérkuti Anna, Hajdu 046 Ákos, Makovsky Mihály, Mamuzsics Gergő Bence, Ónodi Gergely, Pécsi 117 Ildikó, Pszota Máté, Szabó 199 Márton, Szentivánszki Soma , Szigeti Zsófia, Tófalusi Ádám. 2 pontot kapott: 7 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 1 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2017. februári fizika feladatai
