A P. 4941. feladat (2017. május)

P. 4941. Egy nagy méretű víztározóban \(\displaystyle H\) magasságú a víz. A tározó mellett (annak fenékszintjével azonos magasságban) \(\displaystyle N\) darab henger alakú tartály van, amelyeket egyforma, viszonylag vékony csövek kötnek össze. A tartálysor egyik vége egy vastag csővel a víztározó aljához csatlakozik, a másik végén egy – kezdetben zárt – leeresztő csap található.

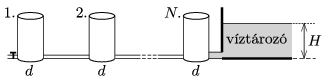
Ha a csapot kinyitjuk, elég hosszú idő után a tartályokban lévő víz össztérfogata \(\displaystyle V_0\) értékkel csökken. Mekkora a tartályok átmérője? (A csövekben a víz súrlódva áramlik.)

Daniel Schumayer (Dunedin, Új-Zéland) feladata

(4 pont)

A beküldési határidő 2017. június 12-én LEJÁRT.

Megoldás. Kezdetben mindegyik tartályban \(\displaystyle H\) magasságú a víz (közlekedőedény elve). Ha kinyitjuk a csapot, a legutolsó tartály gyakorlatilag teljesen kiürül, a legelsőben – jó közelítéssel – marad a \(\displaystyle H\) magasság. A közbenső tartályokban számtani sorozat szerint változik a vízmagasság, hiszen az egyforma hosszú csövekben (az egyensúlyi áramlási állapot beállta után) ugyanannyit esik a nyomás. A vízmagasságok tehát:

\(\displaystyle 0, \quad \frac{1}{N-1}H, \quad \frac{2}{N-1}H,\ldots , \frac{N-1}{N-1}H,\)

a tartályokban lévő víz térfogata pedig:

\(\displaystyle NH\frac{d^2\pi}{4}-V_0=\frac{d^2\pi}{4}\frac{H}{(N-1)}\,(1+2+\ldots +(N-1)), \)

ahonnan

\(\displaystyle d=\sqrt{\frac{8V_0}{H\pi N}}.\)

Statisztika:

9 dolgozat érkezett.
4 pontot kapott:	Bukor Benedek, Fekete Balázs Attila, Kolontári Péter, Mamuzsics Gergő Bence, Molnár Mátyás, Morvai Orsolya, Páhoki Tamás, Tófalusi Ádám.
3 pontot kapott:	Pszota Máté.

A KöMaL 2017. májusi fizika feladatai