 |
A P. 4969. feladat (2017. október) |
P. 4969. Két lapos tekercs közös szimmetriatengelyen, egymástól \(\displaystyle h\) távolságra az ábrán látható módon helyezkedik el. A tekercsek menetszáma \(\displaystyle N_1\), illetve \(\displaystyle N_2\), sugaruk \(\displaystyle R\) és \(\displaystyle r\) (\(\displaystyle r\ll R\)), valamint \(\displaystyle I_1\), illetve \(\displaystyle I_2\) erősségű áram folyik bennük. Mekkora erőt fejt ki egymásra a két tekercs?
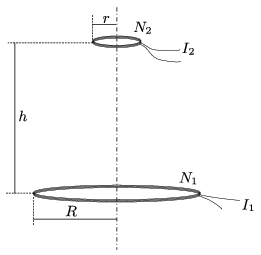
A Kvant nyomán
(6 pont)
A beküldési határidő 2017. november 10-én LEJÁRT.
Megoldás. A Biot–Savart-törvény szerint számolható a nagyobb tekercs \(\displaystyle B(x)\) mágneses indukciója a szimmetriatengely mentén. (Ez a képlet a ,,Négyjegyűben'' is megtalálható.)
\(\displaystyle B(x)=\frac{\mu_0}2 \frac{I_1N_1R^2}{\left(x^2+R^2\right)^{3/2}}.\)
A kis tekercs áramjárta meneteire ható eredő erő – a tengelyes szimmetria miatt – csakis a két tekercs közös szimmetriatengelyével párhuzamos lehet. Ilyen erőt a mágneses tér sugár irányú (a szimmetriatengelyre merőleges) \(\displaystyle B_r\) indukcióvektor-komponense hoz létre:
\(\displaystyle F=B_r\cdot N_2I_2\cdot 2\pi r.\)
\(\displaystyle B_r\) nagysága abból a feltételből határozható meg, hogy a mágneses indukciómező forrásmentes (hiszen mágneses töltések nincsenek). Ha elképzelünk egy \(\displaystyle r\) sugarú, kicsiny \(\displaystyle \Delta h\) magasságú hengert a kis tekercs helyén, abba az egyik alapkörén \(\displaystyle r^2\pi B(h)\) számú erővonal lép be, a távolabbi alapkörén \(\displaystyle r^2\pi B(h+\Delta h)\) számú erővonal lép ki, és a palástján további \(\displaystyle 2r\pi \Delta h\cdot B_r\) számú erővonal lép ki. A mágneses indukció forrásmentességének feltétele:
\(\displaystyle r^2\pi B(h)=r^2\pi B(h+\Delta h)+2r\pi \Delta h\cdot B_r,\)
vagyis
\(\displaystyle B_r=\frac{r}{2}\frac{B(h+\Delta h)-B(h)}{\Delta h}.\)
A fenti képletben szereplő tört az \(\displaystyle (1+\varepsilon)^n\approx 1+n\varepsilon\) (\(\displaystyle \varepsilon\ll 1\)) közelítő formula segítségével, esetleg deriválással számolható:
\(\displaystyle \frac{B(h+\Delta h)-B(h)}{\Delta h}\approx B'(x)\vert _{(x=h)}=-\mu_0\frac32 \, \frac{ I_1N_1R^2h}{ \left(h^2+R^2\right)^{5/2}}.\)
Így végül a keresett erő kifejezése:
\(\displaystyle F=\mu_0\frac{3\pi }2R^2r^2I_1I_2N_1N_2\frac{h}{(h^2+R^2)^{5/2}}.\)
Statisztika:
10 dolgozat érkezett. 6 pontot kapott: Elek Péter, Marozsák Tóbiás , Olosz Adél, Tófalusi Ádám. 3 pontot kapott: 2 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2017. októberi fizika feladatai
