 |
A P. 4983. feladat (2017. december) |
P. 4983. Rögzített, hővezető falú, zárt tartály belsejéhez az ábra szerint egy hőszigetelt falú henger van erősítve. A hengerben lévő 1 dm\(\displaystyle ^2\) keresztmetszetű, hőszigetelő dugattyú súrlódásmentesen mozoghat. Kezdetben a hengerben is és a tartályban is 2,6 dm\(\displaystyle {}^3\) térfogatú, \(\displaystyle 10^5\) Pa nyomású és 27 \(\displaystyle ^\circ\)C hőmérsékletű levegő van.
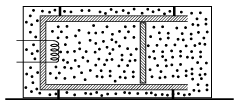
A hengerben lévő levegőt egy fűtőszállal melegíteni kezdjük, eközben a tartályban lévő levegő hőmérséklete állandó marad.
\(\displaystyle a)\) Mennyivel mozdul el a dugattyú, ha a hengerben lévő levegő hőmérséklete 77 \(\displaystyle ^\circ\)C-ra nő?
\(\displaystyle b)\) Ábrázoljuk vázlatosan a hengerben lévő gáz állapotváltozását a \(\displaystyle p\)–\(\displaystyle V\) állapotsíkon!
\(\displaystyle c)\) Becsüljük meg, mennyi hőt vesz fel a hengerben lévő levegő!
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2018. január 10-én LEJÁRT.
Megoldás. \(\displaystyle a)\) A hengerben lévő gáz kezdeti adatait a szokásos módon \(\displaystyle p_0, V_0\) és \(\displaystyle T_0\)-lal jelöljük, a megváltozott értékeket pedig \(\displaystyle p, V\) és \(\displaystyle T\)-vel, a tartályban lévő levegő adatai ekkor: \(\displaystyle p, 2V_0-V\) és \(\displaystyle T_0\), hiszen a dugattyú két oldalán a nyomások megegyeznek, és az össztérfogat is állandó. Felírhatjuk az általános gáztörvényt mindkét levegőmennyiségre:
\(\displaystyle \frac{pV}{T}=\frac{p_0V_0}{T_0}, \qquad p(2V_0-V)=p_0V_0.\)
Innen kiszámítható, hogy
\(\displaystyle V=\frac{2T}{T-T_0}V_0=\frac{2\cdot 350}{350-300}\,2{,}6~{\rm dm}^3=2{,}8~{\rm dm}^3,\)
a hengerben lévő levegő térfogata 0,2 \(\displaystyle {\rm dm}^3\)-rel növekszik, vagyis a dugattyú 2 cm-rel mozdul el.
\(\displaystyle b)\) Az állapotváltozás a \(\displaystyle p-V\) diagramon a
\(\displaystyle p(V)=\frac{p_0V_0}{2V_0-V}\)
összefüggésnek megfelelően egy hiperbolával adható meg.
\(\displaystyle c)\) Az első főtétel szerint a felvett hő (kicsiny változások esetén)
\(\displaystyle Q=\Delta E+W'=\frac52\Delta(pV)+p\Delta V=\frac72p\Delta V+\frac52V\Delta p.\)
Mivel esetünkben \(\displaystyle p\) és \(\displaystyle V\) viszonylag keveset változik, a felvett hőt egyetlen lépésben kiszámíthatjuk (a képletben \(\displaystyle p\) és \(\displaystyle V\) helyébe a kezdeti és a megváltozott értékek számtani közepét helyettesíthetjük). Az így becsült érték: \(\displaystyle Q\approx 0{,}13\) kJ.
Statisztika:
61 dolgozat érkezett. 5 pontot kapott: Andorfi István, Bíró Dániel, Bukor Benedek, Csire Roland, Csuha Boglárka, Elek Péter, Fajszi Bulcsú, Fekete Balázs Attila, Guba Zoltán, Háder Márk István, Jánosik Áron, Kolontári Péter, Kondákor Márk, Kozák András, Lipták Gergő, Magyar Róbert Attila, Marozsák Tóbiás , Máth Benedek, Morvai Orsolya, Németh Csaba Tibor, Olosz Adél, Ónodi Gergely, Pszota Máté, Sal Dávid, Schneider Anna, Takács Árpád, Tófalusi Ádám, Viczián Anna. 4 pontot kapott: Balogh Tamás, Bartók Imre, Berke Martin, Bonifert Balázs, Czett Mátyás, Édes Lili, Garamvölgyi István Attila, Jánosdeák Márk, Keltai Dóra, Klučka Vivien, Mamuzsics Gergő Bence, Markó Gábor, Molnár Mátyás, Pálfi Fanni, Póta Balázs, Rusvai Miklós, Shirsha Bose, Surján Botond, Tafferner Zoltán, Turcsányi Máté, Zirci Márton. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 3 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2017. decemberi fizika feladatai
