A P. 5039. feladat (2018. május)

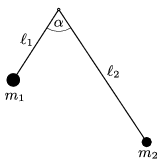
P. 5039. Két könnyű, merev pálca hossza \(\displaystyle \ell_1\), illetve \(\displaystyle \ell_2\). Egyik végükhöz \(\displaystyle m_1\), illetve \(\displaystyle m_2\) tömegű, kis méretű testet erősítünk, másik végüket mereven összekötjük úgy, hogy a pálcák egymással bezárt szöge \(\displaystyle \alpha\) legyen. Ez a rendszer az összekötési ponton átmenő, vízszintes tengely körül szabadon lenghet a pálcák által meghatározott síkban. Mekkora az egyensúlyi helyzetéből kissé kitérített rendszer lengésideje?

Példatári feladat

(5 pont)

A beküldési határidő 2018. június 11-én LEJÁRT.

Megoldás. A rendszer egy fizikai inga, melynek tehetetlenségi nyomatéka a forgástengelyre vonatkoztatva

\(\displaystyle \Theta=m_1\ell_1^2+m_2\ell_2^2,\)

a tömegközéppontja pedig

\(\displaystyle d=\frac{\sqrt{m_1^2\ell_1^2+m_2^2\ell_2^2+2m_1m_2\ell_1\ell_2\cos\alpha}}{m_1+m_2}\)

távol van a forgástengelytől. Ez utóbbi összefüggést úgy láthatjuk be, hogy a tömegközéppontba mutató

\(\displaystyle {\boldsymbol d} =\frac{m_1}{m_1+m_2}{\boldsymbol \ell}_1+\frac{m_2}{m_1+m_2}{\boldsymbol \ell}_2\)

vektor önmagával vett skalárszorzatát képezzük, vagy a koszinusztételt alkalmazzuk az

\(\displaystyle \frac{m_1\ell_1}{m_1+m_2} \qquad \text{és} \qquad \frac{m_2\ell_2}{m_1+m_2}\)

oldalú, \(\displaystyle 180^\circ-\alpha\) szögű háromszögre.

A rendszer lengésideje:

\(\displaystyle T=2\pi\sqrt{ \frac{\Theta}{\left(m_1+m_2\right)gd} }=2\pi\sqrt{ \frac{m_1\ell_1^2+m_2\ell_2^2}{g\sqrt{m_1^2\ell_1^2+m_2^2\ell_2^2+2m_1m_2\ell_1\ell_2\cos\alpha}}}. \)

Statisztika:

19 dolgozat érkezett.
5 pontot kapott:	Bukor Benedek, Édes Lili, Fekete Balázs Attila, Jánosik Áron, Kolontári Péter, Lipták Gergő, Mamuzsics Gergő Bence, Markó Gábor, Marozsák Tóbiás , Molnár Mátyás, Morvai Orsolya, Olosz Adél, Póta Balázs, Sal Dávid.
4 pontot kapott:	Turcsányi Ádám.
3 pontot kapott:	3 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2018. májusi fizika feladatai