 |
A P. 5041. feladat (2018. május) |
P. 5041. Vízszintes síkban, egymástól \(\displaystyle L= 10\) cm távolságra két párhuzamos, elhanyagolható ellenállású, rögzített sín van, amelyeket az ábra szerint az egyik végüknél \(\displaystyle U_0= 0{,}3\) V-os, állandó feszültségű áramforrás kapcsol össze. A ,,berendezés'' függőlegesen lefelé mutató, \(\displaystyle B=1\) T indukciójú, homogén mágneses mezőben van. A sínekre merőlegesen \(\displaystyle R=0{,}2~\Omega\) ellenállású fémpálcát fektettünk, ami a síneken súrlódásmentesen mozoghat.
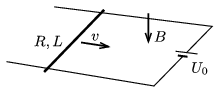
Mekkora nagyságú és milyen irányú erőt kell a sínekkel párhuzamosan kifejteni a pálcára, hogy az az ábrán jelzett irányban állandó \(\displaystyle v\) sebességgel mozogjon, ha
\(\displaystyle a)\) \(\displaystyle v=1\) m/s;
\(\displaystyle b)\) \(\displaystyle v=5\) m/s?
\(\displaystyle c)\) Mekkora a telep által leadott teljesítmény a két esetben?
Közli: Zsigri Ferenc, Budapest
(5 pont)
A beküldési határidő 2018. június 11-én LEJÁRT.
Megoldás. Jelöljük a fémpálcát egyenletes sebességgel mozgató ember által kifejtett erőt \(\displaystyle F\)-fel, a pálcán, a síneken és a telepen átfolyó áram erősséget pedig \(\displaystyle I\)-vel, az ábrán jelölt irányokat tekintve pozitívnak. (Ha az áram vagy az erő tényleges iránya az ábrán jelölttel ellentétes lenne, azt a megfelelő fizikai mennyiségek negatív előjele fogja jelezni.)
A mozgó fémpálcában \(\displaystyle U_1=BLv\) nagyságú feszültség indukálódik, ami (és a telep feszültsége) együttesen
\(\displaystyle I=\frac{U_0-BLv}{R}\)
áramot hoz létre. Az áramjárta, mozgó pálcára a mágneses mező \(\displaystyle F=BIL\) nagyságú erőt fejt ki, ami (\(\displaystyle I>0\) esetén) a telep irányába húzza a pálcát. Az egyenletes mozgás fenntartásához a pálcát mozgató embernek a teleppel ellentétes irányban, balra kell húznia a fémpálcát, ahogy azt az ábra mutatja.

Az ember által kifejtett teljesítmény:
\(\displaystyle P_\text{ember}=-Fv=-BILv=\frac{BLv-U_0}{R}BLv=\frac{(BLv)^2 }{R}-\frac{BLv}{R} U_0.\)
Másrészt a telep által leadott teljesítmény:
\(\displaystyle P_\text{telep}=U_0I=\frac{U_0^2}{R}-\frac{BLv}{R} U_0.\)
Ennek a két teljesítménynek az összege éppen az \(\displaystyle R\) ellenálláson időegységenként fejlődő Joule-hővel egyezik meg:
\(\displaystyle P_\text{ember}+ P_\text{telep}=\frac{(U_0-BLv)^2}{R}=I^2R=P_\text{Joule},\)
tehát a munkatétel általánosított alakja a jelen esetben is teljesül.
\(\displaystyle a)\) \(\displaystyle v=1\) m/s esetén \(\displaystyle I=1{,}0~\rm A\), \(\displaystyle F=0{,}1~\rm N\), így
\(\displaystyle P_\text{ember}=-0{,}1~{\rm W};\qquad P_\text{telep}=+0{,}3~{\rm W};\qquad P_\text{Joule}=+0{,}2~{\rm W}.\)
A telep több munkát végez, mint a fejlődő Joule-hő, a különbözet az emberen végzett munkával egyezik meg.
\(\displaystyle b)\) \(\displaystyle v=5\) m/s esetén \(\displaystyle I=-1{,}0~\rm A\), \(\displaystyle F=-0{,}1~\rm N\), továbbá
\(\displaystyle P_\text{ember}= 0{,}5~{\rm W};\qquad P_\text{telep}=-0{,}3~{\rm W};\qquad P_\text{Joule}=+0{,}2~{\rm W}.\)
Az ember most több munkát végez, mint a Joule-hő, a különbözetet a telep (akkumulátor) veszi fel, annak energiáját növeli.
Statisztika:
29 dolgozat érkezett. 5 pontot kapott: Bukor Benedek, Csire Roland, Debreczeni Tibor, Illés Gergely, Marozsák Tóbiás , Máth Benedek, Olosz Adél, Sal Dávid, Vaszary Tamás. 4 pontot kapott: Bartók Imre, Édes Lili, Elek Péter, Fajszi Bulcsú, Kondákor Márk, Lipták Gergő, Makovsky Mihály, Markó Gábor, Molnár Mátyás, Morvai Orsolya, Rusvai Miklós, Tafferner Zoltán, Turcsányi Ádám. 3 pontot kapott: 3 versenyző. 2 pontot kapott: 4 versenyző.
A KöMaL 2018. májusi fizika feladatai
