A P. 5057. feladat (2018. október)

P. 5057. Egy \(\displaystyle \alpha=30^\circ\) hajlásszögű lejtőre helyezünk egy \(\displaystyle m=0{,}5\) kg tömegű és egy \(\displaystyle 3m\) tömegű kicsiny testet, amelyek elhanyagolható tömegű, \(\displaystyle d=50\) cm hosszúságú, merev rúddal vannak összekapcsolva. A lejtő felső része súrlódásmentes, az alsó részén a súrlódási együttható \(\displaystyle \mu=0{,}2\).

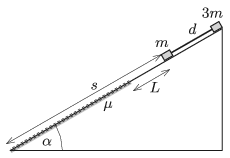
Kezdetben az \(\displaystyle m\) tömegű test \(\displaystyle L=40\) cm távolságra van attól a határvonaltól, ahol már van súrlódás, és \(\displaystyle s=120\) cm távol van a lejtő aljától. A két (pontszerűnek tekinthető) testből álló rendszert magára hagyjuk.

\(\displaystyle a)\) Adjuk meg a rúdban ébredő erőt a megtett út függvényében!

\(\displaystyle b)\) Mennyi idő alatt ér le az \(\displaystyle m\) tömegű test a lejtő aljára?

Közli: Kotek László, Pécs

(5 pont)

A beküldési határidő 2018. november 12-én LEJÁRT.

Megoldás. A mozgás három szakaszra osztható.

1. Ha a megtett út kisebb, mint \(\displaystyle L\), mindkét test a lejtő súrlódásmentes részén mozog. A rendszer gyorsulása

\(\displaystyle a_1=g\sin\alpha\approx 4{,}905~\frac{\rm m}{\rm s^2},\)

a mozgás ideje pedig

\(\displaystyle t_1=\sqrt{\frac{2L}{g\sin\alpha}}\approx 0{,}404~\rm s.\)

A rendszer sebessége ezen szakasz végén

\(\displaystyle v_1=a_1t_1\approx 1{,}98~\frac{\rm m}{\rm s }.\)

A mozgás ezen szakaszában a rúdban ható erő mindvégig nulla.

2. A második szakaszban az \(\displaystyle m\) tömegű test már súrlódva, a \(\displaystyle 3m\) tömegű súrlódásmentesen mozog. A mozgásegyenletek (a lejtő mentén lefelé mutató irányt tekintve pozitívnak):

\(\displaystyle mg(\sin\alpha-\mu \cos\alpha)+K=ma_2,\)

\(\displaystyle 3mg \sin\alpha-K=3ma_2.\)

A két egyenlet összegéből

\(\displaystyle a_2=g(\sin\alpha-\frac{\mu}{4}\cos\alpha)\approx 4{,}48~\frac{\rm m}{\rm s^2},\)

a rudat feszítő (összenyomó) erő:

\(\displaystyle K=mg\frac{3\mu}{4}\cos\alpha\approx 0{,}64~\rm N.\)

A rendszer sebessége ezen szakasz végén (pl. a munkatételből számolva):

\(\displaystyle v_2=\sqrt{v_1^2+2a_2d}\approx 2{,}90~\frac{\rm m}{\rm s},\)

a mozgás ideje pedig a második szakaszban:

\(\displaystyle t_2=\frac {v_2-v_1}{a_2}= 0{,}205~ {\rm s}.\)

3. A harmadik, \(\displaystyle s-L-d=0{,}3~\rm m\) hosszú szakaszon a rendszer gyorsulása:

\(\displaystyle a_3=g(\sin\alpha-\mu\cos\alpha)\approx 3{,}21~\frac{\rm m}{\rm s^2 },\)

a végsebesség pedig

\(\displaystyle v_3=\sqrt{v_2^2+2a_3(s-L-d)}\approx3{,}21~\frac{\rm m}{\rm s}.\)

A mozgás ideje ezen szakaszon:

\(\displaystyle t_3=\frac{v_3-v_2}{a_3}= 0{,}10~ {\rm s},\)

és a rúdban most nem alakul ki mechanikai feszültség.

A mozgás teljes időtartama: \(\displaystyle T=t_1+t_2+t_3\approx0{,}71~ \rm s.\)

Statisztika:

89 dolgozat érkezett.
5 pontot kapott:	Bekes Barnabás, Boros Máté, Bukor Benedek, Conrád Márk, Csépányi István, Fiam Regina, Fonyi Máté Sándor, Fülöp Sámuel Sihombing, Hartmann Alice, Jánosik Áron, Kardkovács Levente, Kárpáti Kristóf, Köpenczei Csanád, Köpenczei Csenge, Kupás Lőrinc, Lipták Gergő, Mácsai Dániel, Makovsky Mihály, Markó Gábor, Marozsák Tádé, Merkl Gergely, Merkl Levente, Morvai Orsolya, Murányi Albert, Nagyváradi Dániel, Olosz Adél, Rozgonyi Gergely, Sal Dávid, Schäffer Bálint, Szabó 314 László, Szoboszlai Szilveszter, Tafferner Zoltán, Telek Dániel, Tiefenbeck Flórián, Toronyi András, Varga Vázsony, Viczián Anna, Virág Levente.
4 pontot kapott:	24 versenyző.
3 pontot kapott:	16 versenyző.
2 pontot kapott:	4 versenyző.
1 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	2 dolgozat.

A KöMaL 2018. októberi fizika feladatai