 |
A P. 5064. feladat (2018. október) |
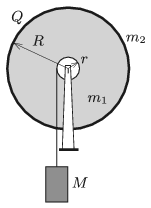
P. 5064. Az ábrán látható, súrlódásmentesen tengelyezett, \(\displaystyle R=20\) cm sugarú, \(\displaystyle m_1=0{,}2\) kg tömegű, tömör szigetelőkorong peremére \(\displaystyle m_2=0{,}05\) kg tömegű rézgyűrűt erősítettünk, amelynek \(\displaystyle Q=8\cdot10^{-6}\) C töltést adtunk. A korong tengelyére rögzített, \(\displaystyle r=5\) cm sugarú csigára tekert vékony fonálon egy \(\displaystyle M=10\) kg tömegű nehezék függ, amelyet egy adott pillanatban lökésmentesen elengedünk. Indítás után \(\displaystyle t=3\) s múlva mekkora lesz a korong keltette mágneses indukció a korong közepénél? (Az önindukció jelensége figyelmen kívül hagyható.)
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2018. november 12-én LEJÁRT.
Megoldás. A korong és a rézgyűrű tehetetlenségi nyomatéka
\(\displaystyle \Theta=\left(\frac{1}{2}m_1+m_2\right)R^2=0{,}006~\rm kg\,m^2.\)
Ha a fonalat \(\displaystyle K\) erő feszíti, akkor a mozgásegyenletek:
\(\displaystyle Mg-K=Ma,\qquad Kr=\Theta\beta,\qquad a=r\beta.\)
Innen a korong szöggyorsulása:
\(\displaystyle \beta=\frac{Mgr}{\Theta+Mr^2}=158~\frac{1}{\rm s^2},\)
a szögsebessége pedig \(\displaystyle t=3~\)s múlva
\(\displaystyle \omega=\beta t=475~\frac{1}{\rm s }.\)
A \(\displaystyle Q\) töltésű rézgyűrű \(\displaystyle T=2\pi/\omega\) idő alatt fordul körbe, vagyis a kerület mentén mozgő töltés
\(\displaystyle I=\frac{Q \omega}{2\pi}=\frac{Q \beta t}{2\pi}=0{,}604~\rm mA\)
áramot képvisel. Ekkora áram a körvezető középpontjában
\(\displaystyle B=\frac{\mu_0I}{2R}=1{,}9\cdot10^{-9} ~\rm T\)
mágneses indukciót hoz létre az adott időpontban.
Megjegyzés. A korong szögsebessége időben növekszik, így a forgás által keltett mágneses indukció is egyre nagyobb lesz. A rézgyűrűn átmenő mágneses fluxus időben változik, ez feszültséget indukál és áramot indít el a rézgyűrűben. Ez az önindukciós eredetű (konduktív) áram (a réz fajlagos ellenállását és a rézgyűrűnek a tömegéből és a hosszából kiszámítható reális keresztmetszetét figyelembe véve) több nagyságrenddel kisebb, mint az elektromosan töltött gyűrű forgásából adódó (konvektív) áram. Jogosan utalt tehát a feladat szövege arra, hogy az önindukciós jelenség figyelmen kívül hagyható.
Statisztika:
34 dolgozat érkezett. 5 pontot kapott: Bonifert Balázs, Bukor Benedek, Gulácsi Máté, Jánosik Áron, Kupás Lőrinc, Lipták Gergő, Makovsky Mihály, Molnár Mátyás, Morvai Orsolya, Olosz Adél, Sal Dávid, Székely Bálint, Vaszary Tamás. 4 pontot kapott: Andorfi István, Békési Ábel, Csépányi István, Hervay Bence, Hubay Csenge, Markó Gábor, Máth Benedek, Pácsonyi Péter, Rusvai Miklós, Tafferner Zoltán, Vass Bence. 3 pontot kapott: 8 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző.
A KöMaL 2018. októberi fizika feladatai
