 |
A P. 5070. feladat (2018. november) |
P. 5070. Egy \(\displaystyle \ell\) magasságú barlangban \(\displaystyle D\) rugóállandójú, feszítetlen állapotában \(\displaystyle d<\ell\) hosszúságú, elhanyagolható tömegű rugó helyezkedik el függőleges helyzetben. A rugó egyik végét a barlang mennyezetéhez, a másik végét pedig a talajhoz rögzítették az ábrán látható módon.
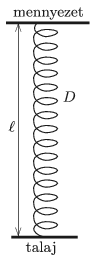
A rugó közepére rárepül és a rugóba kapaszkodik egy \(\displaystyle m\) tömegű, kis méretű denevér, és a rugó vezérelte bonyolult rezgésbe kezd. (A denevér mozgása során a rugó semelyik darabja nem lazul meg.)
\(\displaystyle a)\) Hol fog megállni a denevér a rezgés lecsillapodása után? (A rugó még nagy megnyújtásnál is követi a Hooke-törvényt.)
\(\displaystyle b)\) Innen a denevér igen óvatosan visszamászik újra a talajtól mért \(\displaystyle \ell/2\) magasságra. Legalább mekkora munkát végez eközben?
Közli: Balogh Péter, Gödöllő
(5 pont)
A beküldési határidő 2018. december 10-én LEJÁRT.
Megoldás. Tekintsük a megfeszített, de egyébként még terheletlen rugó egy olyan \(\displaystyle P\) pontját, amely a mennyezettől \(\displaystyle \ell_1\), a talajtól pedig \(\displaystyle \ell_2\) távolságban van (lásd az ábrát). Nyilván \(\displaystyle \ell_1+\ell_2=\ell\). Számítsuk ki, hogy mekkora \(\displaystyle x\) távolsággal süllyed le a rugó ezen pontja, ha ott \(\displaystyle F\) nagyságú, függőlegesen lefelé ható erőt fejtünk ki a rugóra.

A rugó \(\displaystyle P\) feletti részének nyújtatlan hossza \(\displaystyle d_1\), az alsó rugódarabé pedig \(\displaystyle d_2\). Nyilván fennáll, hogy \(\displaystyle d_1+d_2=d\), és mivel az egyes rugórészekre és a teljes rugóra is ugyanakkora erő hat denevér nélkül:
\(\displaystyle \frac{d}{d_1}=\frac{\ell}{\ell_1},\qquad \frac{d}{d_2}=\frac{\ell}{\ell_2}.\)
A felső rugó megnyúlása
\(\displaystyle \ell_1+x-d_1=d_1\left(\frac\ell{d}-1\right)+x,\)
a benne ébredő erő tehát
\(\displaystyle F_1=D\frac{d}{d_1}d_1\left(\frac\ell{d}-1\right)+D\frac{d}{d_1}x=D(\ell-d)+D\frac{\ell}{\ell_1}x.\)
Felhasználtuk, hogy a rugó felső részének megfelelő rugódarab rugóállandója a hosszával fordítottan arányos, esetünkben tehát \(\displaystyle D_1=Dd/d_1=D\ell/\ell_1\), és hasonlóan az alsó rész rugóállandója \(\displaystyle D_2=D\ell/\ell_2\). Ennek megfelelően az alsó rugódarab által (függőlegesen lefelé) kifejtett erő:
\(\displaystyle F_2=D(\ell-d)-D\frac{\ell}{\ell_2}x,\)
vagyis a teljes külső erő és a \(\displaystyle P\) pont elmozdulása közötti kapcsolat:
\(\displaystyle F(x)=F_1-F_2=D\left(\frac{\ell}{\ell_1}+\frac{\ell}{\ell_2}\right) x.\)
Megjegyzés: A megfeszített rugó éppen úgy viselkedik, mint egy \(\displaystyle D\) rugóállandójú, \(\displaystyle \ell\) hosszúságú, kezdetben feszítetlen rugó. Ez utóbbi azonban húzó-nyomó rugó kell hogy legyen, hiszen az alsó rugó függőlegesen lefelé ható erő esetén megrövidül, benne nyomófeszültségek alakulnak ki. Az előfeszítés azt eredményezi, hogy a könnyebben megvalósítható ,,húzó'' rugóval is létrehozható (nem túl nagy deformációk esetén) úgy a felfelé, mind pedig a lefelé ható eredő erő.
A továbbiakban vizsgáljuk meg, mekkora \(\displaystyle x\) távolsággal süllyed le a rugó felezőpontja felett \(\displaystyle y\) távolságban elhelyezett \(\displaystyle mg\) súlyú test (a denevér) az egyensúlyi állapotában. Ilyenkor
\(\displaystyle \ell_1=\frac{\ell}{2}-y,\qquad \ell_2=\frac{\ell}{2}+y,\)
az egyensúly feltétele tehát
\(\displaystyle D\ell\left(\frac{1}{\frac{\ell}{2}-y }+\frac{1}{\frac{\ell}{2}+y }\right) x=mg,\)
vagyis
\(\displaystyle \ell x=\frac{mg}{D\ell}\left(\frac{\ell^2}{4}-y^2\right).\)
Célszerű bevezetni a dimenziótlan
| \(\displaystyle (1)\) | \(\displaystyle \lambda \equiv\frac{mg}{D\ell}\) |
jelölést, ezzel az \(\displaystyle y\) és \(\displaystyle x\) közötti kapcsolat:
| \(\displaystyle (2)\) | \(\displaystyle x=\lambda\frac{\ell}{4}-\lambda\frac{y^2}{\ell}.\) |
\(\displaystyle a)\) Ha \(\displaystyle \ell/2\) magasan lévő pontba repül a denevér, ami az \(\displaystyle y=0\) esetnek felel meg, akkor az egyensúly beállta után (1) és (2) szerint
| \(\displaystyle (3)\) | \(\displaystyle x=\frac{\lambda}{4}\ell=\frac{mg}{4D}\) |
távolsággal kerül lejjebb.
Megjegyzés. Feltételeztük, hogy \(\displaystyle x<(\ell-d)/2\) (vagyis a rugó előfeszítettsége elegendően nagy, és így a denevér alatt lévő rugódarab még az egyensúlyi állapotban is feszes marad).
\(\displaystyle b)\) Ha a denevér nagyon lassan, óvatosan felmászik a rugónak egy olyan \(\displaystyle P\) pontjába, amely – ha a deformáltság a rugó mentén mindenhol ugyanakkora lenne – \(\displaystyle y\) távolsággal lenne magasabban a felezőpontnál, és onnan éppen \(\displaystyle x=y\) távolsággal süllyed le, akkor a talajtól mért távolsága továbbra is \(\displaystyle \ell/2\) maradna. A (2) egyenlet számunkra érdekes \(\displaystyle y>0\) megoldása \(\displaystyle x=y\) esetén:
| \(\displaystyle (4)\) | \(\displaystyle y=\frac{\ell}{2\lambda}\left(\sqrt{1+\lambda^2}-1\right)=\frac{D\ell^2}{2mg}\left(\sqrt{1+\frac{m^2g^2}{D^2\ell^2}}-1\right).\) |
Megjegyzés: Ha a rugó a denevér súlyához képest viszonylag erős, vagyis \(\displaystyle D\ell \gg mg,\) akkor \(\displaystyle y\ll \ell\) és \(\displaystyle D_1\approx D_2\approx 2D\), a denevér által okozott rugómegnyúlás \(\displaystyle y\approx mg/(4D)\), ami éppen az \(\displaystyle a)\) alkérdésben szereplő \(\displaystyle x\)-szel egyenlő.
A denevér mászása közben az egész rendszer energiájának megváltozása (a denevér gravitációs helyzeti energiájának változása és a rugók rugalmas energiájának változása) így adható meg:
\(\displaystyle \Delta E=mgx+\frac{1}{2}\left(D_1+D_2\right)\,y^2-\frac{1}{2}\left(2D\right)\,2x^2= \frac{(mg)^2}{8D}+\frac{D\ell^2}{4}\left(\sqrt{1+\frac{m^2g^2}{D^2\ell^2}}-1\right).\)
Erős rugó határesetben \(\displaystyle \Delta E={m^2g^2}/(4D).\)
Megjegyzés: A mechanikai energiaváltozást az egyszerűbb
\(\displaystyle \Delta E=\frac{mg}{2}(x+y)\)
képlet alapján is ki lehet számítani, ahol \(\displaystyle x\)-et és \(\displaystyle y\)-t természetesen ki kell fejezni (3).nak és (4)-nek megfelelően \(\displaystyle D\), \(\displaystyle mg\) és \(\displaystyle \ell\) segítségével. A képlet szemléletes jelentése a következő. A denevér és a rugórendszer kezdeti energiája az \(\displaystyle \ell/2\) magasságból \(\displaystyle x\) távolságnyit lassan (gyorsulásmentesen) lesüllyesztett testen végzett munkával egyenlő. (A rugalmas energiát a terheletlen, de megfelelően előfeszített állapotban választjuk nullának, a helyzeti energia nullpontját pedig a rugó felezőpontjához igazítjuk.) A végzett munka az átlagos \(\displaystyle mg/2\) erő és az \(\displaystyle x\) elmozdulás előjeles szorzata: \(\displaystyle -mgx/2.\) A felmászás utáni állapot rugalmas energiája azzal a munkával egyenlő, amennyivel a rugó megfelelő \(\displaystyle P\) pontját lassan \(\displaystyle y\) távolsággal lejjebb tudjuk húzni. Ez ismét az átlagos húzóerőből számítható: \(\displaystyle mgy/2\). A két energia különbsége a denevér által előidézett mechanikai energiaváltozás.
A denevér által végzett munka legalább akkora, mint a mechanikai energia növekedése. Ennél azonban nagyobb is lehet, ha a denevér gyorsan, vagy ugrásszerűen mozog, hiszen ekkor a rugóban rugalmas hullámok keletkezhetnek, amelyek lecsillapodása során hő fejlődik.
Statisztika:
22 dolgozat érkezett. 5 pontot kapott: Markó Gábor, Marozsák Tádé. 4 pontot kapott: Lipták Gergő, Merkl Gergely, Olosz Adél, Sas 202 Mór, Varga Vázsony. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 5 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2018. novemberi fizika feladatai
