 |
A P. 5073. feladat (2018. november) |
P. 5073. Függőleges, igen hosszú (végtelennek vehető) egyenes szigetelőszál lineáris töltéssűrűsége \(\displaystyle \lambda= 8\cdot10^{-7}\) C/m. A száltól \(\displaystyle d_0=5\) cm távolságban igen vékony, \(\displaystyle \ell=10\) cm hosszú szigetelőfonálra felfüggesztünk egy \(\displaystyle m=2\) g tömegű, \(\displaystyle q=7\cdot10^{-8}\) C töltésű, kis méretű fémgolyót. A fonál függőleges állapotában a rögzítést lökésmentesen megszüntetjük.
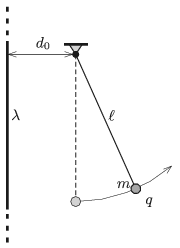
\(\displaystyle a)\) Milyen messzire távolodik el a fémgolyó a szigetelőszáltól?
\(\displaystyle b)\) Mekkora a fonál függőlegessel bezárt szöge, amikor a golyó sebessége maximális? Mekkora ez a maximális sebesség?
\(\displaystyle c)\) Mekkora erő hat a felfüggesztésre, amikor leggyorsabban mozog a golyó?
Közli: Holics László, Budapest
(5 pont)
A beküldési határidő 2018. december 10-én LEJÁRT.
Megoldás. A szigetelőszál körül az elektromos térerősség ,,radiális'', és a nagysága a száltól \(\displaystyle r\) távolságban (az elektrosztatikai Gauss-törvény szerint)
\(\displaystyle E(r)=\frac{2k\lambda}{r}.\)
Ez a térerősség az
\(\displaystyle U(r)=- 2k\lambda \ln \frac{r}{r_0} \)
potenciálnak felel meg, amint az integrálszámítással, vagy a hőtani analógia alapján (az izotermikus munkavégzés képlete alapján) látható be. A potenciál nullpontját önkényesen választott \(\displaystyle r_0\) távolsághoz illesztettük, ez a távolság lehet például a fonál függőleges helyzetének megfelelő \(\displaystyle d_0\) érték.
Jelöljük a fonál függőlegessel bezárt szögét \(\displaystyle x\)-szel, és alkalmazzuk az energiamegmaradás tételét! Mivel a szigetelőszáltól mért távolság
\(\displaystyle d=d_0+\ell\sin x,\)
fennáll
\(\displaystyle \frac{1}{2}mv^2+mg\ell(1-\cos x)-2kq\lambda \ln \frac{d}{d_0}=0,\)
vagyis
\(\displaystyle f(x)\equiv v^2(x)=\frac{4kq\lambda}{m}\, \ln\left( 1+\frac{\ell}{d_0}\sin x\right)-2g\ell(1-\cos x).\)
A megadott mennyiségeket behelyettesítve (SI-egységrendszerben számolva)
\(\displaystyle f(x)=\ln\left( 1+2\sin x\right)-1{,}96\,(1-\cos x).\)
\(\displaystyle a)\) A fémgolyó legnagyobb eltávolodását, vagyis a megállását jellemző szöget az \(\displaystyle f(x)=0\) egyenlet \(\displaystyle (x>0)\) gyöke adja meg. Grafikus ábrázolással, vagy pl. a http://www.wolframalpha.com segítségével megkaphatjuk, hogy \(\displaystyle x\approx 1{,}05 \) rad, azaz kb. \(\displaystyle 60^\circ\). Ennek megfelelően a fémgömb legfeljebb 13,7 cm-re távolodik el a szigetelőszáltól.
\(\displaystyle b)\) Ugyancsak az \(\displaystyle f(x)\) függvény vizsgálatával, a maximumának megkeresésével kapjuk meg a sebesség legnagyobb értékét. Ez \(\displaystyle x\approx 0{,}49\) radiánnál, azaz \(\displaystyle 28^\circ\)-nál található, és \(\displaystyle v_\text{max}=0{,}66~\)m/s.
\(\displaystyle c)\) A legnagyobb sebességnél a fonalat feszítő erő (Newton mozgástörvénye alapján):
\(\displaystyle F=mg\cos x+\frac{mv_\text{max}^2}{\ell}+\frac{2k\lambda q}{d_0+\ell\sin x}\sin x \approx 0{,}03~\rm N.\)
Statisztika:
29 dolgozat érkezett. 5 pontot kapott: Bekes Barnabás, Békési Ábel, Csépányi István, Makovsky Mihály, Máth Benedek, Molnár Mátyás, Olosz Adél, Sal Dávid, Tiefenbeck Flórián. 4 pontot kapott: Bokor Endre, Elek Péter, Jánosik Áron, Ludányi Levente, Marozsák Tádé, Németh Csaba Tibor, Pácsonyi Péter, Vass Bence, Viczián Anna. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2018. novemberi fizika feladatai
