A P. 5075. feladat (2018. november)

P. 5075. Az ábra szerinti elrendezésben közös optikai tengelyen, egymással párhuzamosan négy vékony lencse helyezkedik el. Mindegyik lencse határfelületének görbületi sugara 5 cm, illetve 10 cm. Kettő közülük \(\displaystyle n=1{,}5\) törésmutatójú üvegben lévő levegőlencse, kettő pedig ugyanilyen törésmutatójú üveglencse.

Az üvegben, az optikai tengelyen, a domborúan homorú lencsétől 60 cm-re egy pontszerű fényforrás van. A lencse másik oldalán, tőle 30 cm távolságra helyezkedik el a homorúan domború levegőlencse. Ettől 10 cm távolságra van az üveget határoló sík felület, amely merőleges az optikai tengelyre. A sík felülettől 10 cm-re található az üvegből készült domborúan homorú lencse, a negyedik (homorúan domború) lencse pedig a harmadiktól 20 cm-re van.

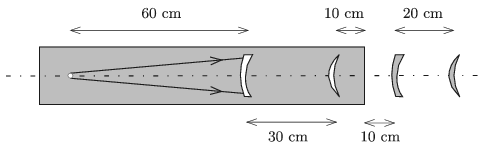
A négy lencse hová képezi le a pontszerű fényforrást?

Közli: Zsigri Ferenc, Budapest

(4 pont)

A beküldési határidő 2018. december 10-én LEJÁRT.

Megoldás. A környezetéhez képest \(\displaystyle n\) relatív törésmutatójú anyagból készült, \(\displaystyle r_1\) és \(\displaystyle r_2\) görbületi sugarú lencse \(\displaystyle f\) fókusztávolságát az

\(\displaystyle \frac{1}{f}=(n-1)\left(\frac{1}{r_1}+\frac{1}{r_2}\right)\)

összefüggésből határozhatjuk meg. (Domború felületek görbületi sugarát pozitív, homorú felületekét pedig negatív előjelűnek tekintjük.) Ennek megfelelően a négy lencse fókusztávolsága balról jobbra haladva:

\(\displaystyle \frac{1}{f_1}=\left(\frac{2}{3}-1\right)\left(\frac{1}{10~\rm cm}-\frac{1}{5~\rm cm}\right) \quad \Rightarrow \quad f_1=+30~\rm cm;\)

\(\displaystyle \frac{1}{f_2}=\left(\frac{2}{3}-1\right)\left(\frac{1}{5~\rm cm}-\frac{1}{10~\rm cm}\right) \quad \Rightarrow \quad f_2=-30~\rm cm;\)

\(\displaystyle \frac{1}{f_3}=\left(\frac{3}{2}-1\right)\left(\frac{1}{10~\rm cm}-\frac{1}{5~\rm cm}\right) \quad \Rightarrow \quad f_3=-20~\rm cm;\)

\(\displaystyle \frac{1}{f_4}=\left(\frac{3}{2}-1\right)\left(\frac{1}{5~\rm cm}-\frac{1}{10~\rm cm}\right) \quad \Rightarrow \quad f_4=+20~\rm cm.\)

\(\displaystyle (i)\) Az első lencse gyűjtőlencse, a kétszeres fókusztávolságra lévő fényforrást a kétszeres fókusztávolságú pontba, vagyis a második lencsétől 30 cm-re jobbra, annak fókuszpontjába képezi le.

\(\displaystyle (ii)\) Erről a látszólagos képről a második lencse (szórólencse) párhuzamos fénysugarakat hoz létre (a kép ,,végtelen távolra'' kerül).

\(\displaystyle (iii)\) A párhuzamos sugarak irányváltoztatás nélkül esnek a harmadik lencsére (ami szórólencse), és azon keresztül úgy haladnak tovább, mintha a lencsétől 20 cm-re balra lévő fókuszpontból indultak volna ki.

\(\displaystyle (iv)\) A harmadik lencse bal oldali fókuszpontja a negyedik (gyűjtő-)lencse kétszeres fókusztávolságú pontja, a kép tehát a negyedik lencsétől jobbra, ugyancsak a kétszeres fókusztávolságú helyen, a lencsétől 40 cm távolságban jön létre.

Statisztika:

22 dolgozat érkezett.
4 pontot kapott:	Bekes Barnabás, Conrád Márk, Gál Péter Levente, Hartmann Alice, Kárpáti Kristóf, Makovsky Mihály, Nagyváradi Dániel, Náray Balázs, Osvárt Bence Attila, Pálfi Fanni, Solymosi Réka, Toronyi András, Zeke Norbert.
3 pontot kapott:	Boros Máté, Kovács Gergely Balázs, Sugár Soma, Szoboszlai Szilveszter.
1 pontot kapott:	4 versenyző.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2018. novemberi fizika feladatai