 |
A P. 5100. feladat (2019. február) |
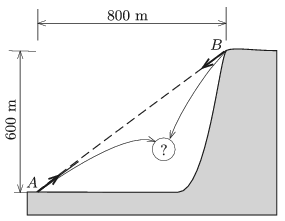
P. 5100. Két ágyúval pontosan ugyanabban a pillanatban tüzelnek egymás felé az ábrán látható \(\displaystyle A\) és \(\displaystyle B\) pontból. Az \(\displaystyle A\) ágyú lövedékének torkolati sebessége 40 m/s, míg a \(\displaystyle B\) ágyúé 60 m/s. Eltalálják-e a lövedékek egymást? Ha igen, akkor hol és mikor? Ha nem, akkor hol csapódnak be a talajba?
Amerikai feladat
(4 pont)
A beküldési határidő 2019. március 11-én LEJÁRT.
Megoldás. Írjuk le a lövedékek mozgását egy olyan koordináta-rendszerből, amelynek origója az \(\displaystyle A\) ágyúnál van, és az \(\displaystyle x\) tengelye vízszintes. A két ágyút összekötő egyenes a vízszintessel \(\displaystyle \alpha=\arctg\frac{600}{800}\approx 37^\circ\)-os szöget zár be, és az \(\displaystyle y\) tengely függőlegesen felfelé mutat.
A lövedékek koordinátái \(\displaystyle t\) idővel a kilövésük után:
\(\displaystyle x_1=\frac{4}{5} \left(40~\frac{\rm m}{\rm s}\right)t,\qquad y_1=\frac{3}{5} \left(40~\frac{\rm m}{\rm s}\right)t-\frac{g}{2}t^2,\)
\(\displaystyle x_2=800~{\rm m}-\frac{4}{5} \left(60~\frac{\rm m}{\rm s}\right)t,\qquad y_2=600~{\rm m}-\frac{3}{5} \left(60~\frac{\rm m}{\rm s}\right)t-\frac{g}{2}t^2.\)
A két lövedék eltalálná egymást, ha \(\displaystyle x_1=x_2\) és \(\displaystyle y_1=y_2\) teljesülne. Formálisan \(\displaystyle t=10~\)s jó megoldásnak látszik, de az összeütközés mégsem jön létre, mert ekkor \(\displaystyle y_1=y_2\approx -250~{\rm m}<0,\) a lövedékek tehát már a találkozásuk előtt a földbe csapódnak. Az \(\displaystyle y_1=0\) feltételből \(\displaystyle t=\)4,9 s és \(\displaystyle x_1=156\) m, \(\displaystyle y_2=0\)-ból pedig \(\displaystyle t_2=\)8,0 s és \(\displaystyle x_2=416~\)m adódik.
Statisztika:
86 dolgozat érkezett. 4 pontot kapott: 53 versenyző. 3 pontot kapott: 18 versenyző. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 8 versenyző. 0 pontot kapott: 2 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2019. februári fizika feladatai
